【数学講師向け】わかりやすく教えよう！数学的帰納法と演繹法

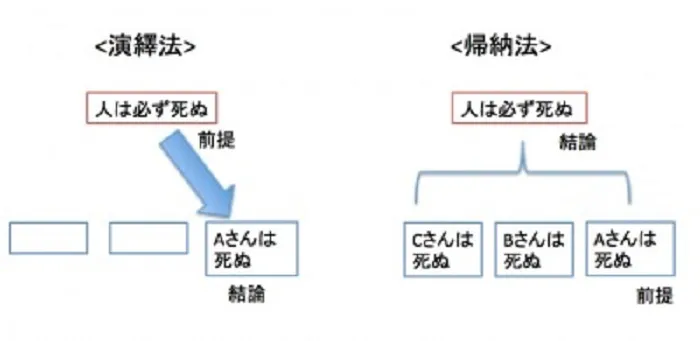
[高校数学]数学的帰納法は演繹法！？

論理展開には、帰納(きのう)法と演繹(えんえき)法があります。
帰納法と演繹法の違いと高校数学で学習する数学的帰納法を紹介します！まずは帰納法からです。

帰納法って何？

帰納法：個別的・特殊的な事例から一般的・普遍的な規則・法則を見出そうとする推論方法のこと。

帰納法には３つの推論が存在します。

<その１：枚挙的帰納法(狭義の帰納法)>
　個々の観察から、それらが所属する集団全体が共通して持つ特徴を導きだすこと。
前提a：一昨日、太陽は東から昇った。
前提b：昨日、太陽は東から昇った。
前提c：今日、太陽は東から昇った。
→結論：太陽は、いつも、東から昇る。

↑帰納法は、枚挙的帰納法のことを意味する場合がほとんどです。

<その２：アナロジー(類推)>
似通った点をもとにして他のことを推量すること。
前提a：レモンソーダは泡立つ。
前提b：ビールはレモンソーダに似ている。
→結論：(たぶん)ビールは泡立つ。

<その３：アブダクション>
起こった現象を最もうまく説明できる仮説を形成するための推論法。
前提a：庭の芝生が濡れている(現象)
前提b：雨が降ると芝生が濡れる(法則)
→結論：（今はやんでいても）雨が降ったに違いない。

↑類推とアブダクションは余り問われません…

帰納法の欠点

・前提が正しくても、結論の正しさは保証されない

導いた結論が正しいという確率は、前提を多く集めるほど高くなります。
昨日と今日、太陽を観測した結果→太陽はいつも東から昇る<結論が正しい可能性が低い>
１年間365日毎日、太陽を観測した結果→太陽はいつも東から昇る<結論が正しい可能性が高い>

・早すぎる一般化

以下の帰納法は間違いです。
"富士山は活火山である。浅間山も活火山である。桜島も活火山である。よって「全ての火山は活火山である」"

少ない例から一般的な結論を導いてしまうことを早すぎる一般化(類推の危険)と呼びます。
この場合、反例を挙げることで、結論の誤りを指摘することができます。

続いては演繹法についてです！

演繹法って何？

演繹法：一般的・普遍的な前提から、より個別的・特殊的な結論を得る推論方法。

<演繹の代表例：三段論法>
公務員試験などでよく見かける、三段論法は演繹法の代表例です。
大前提：人は必ず死ぬ
小前提：ソクラテスは人である
→結論：ソクラテスは必ず死ぬ

以上を記号で書くと、

大前提：人→必ず死ぬ…(a)
小前提：ソクラテス→人…(b)
(a)と(b)の矢印を繋げると、ソクラテス→人→必ず死ぬ
結論：ソクラテス→必ず死ぬ

帰納法と演繹法の違い

・真理保存性の違い
演繹法の結論は、必ず正しい。帰納法の結論は、正しくないかもしれない。

・結論と前提の違い

演繹法

以上をまとめると、

帰納法：個々の事例の共通点から、間違いかもしれない一般的な結論を導く。事例の個数が増えるほど、結論の正しさが高まる。
演繹法：大前提がすでに存在していて、その前提の個々の事例について注目する。大前提は正しいので、個々の事例も正しい。

さて、実際に一般的な帰納法・演繹法の話から進んで数学的帰納法を見てみましょう！

数学的帰納法

<例題>
任意の自然数nについて、
2(1＋２＋…＋n)=n(n＋1)…①
であることを数学的帰納法を用いて証明しなさい。

<答え>
[証明]
[1]n=1のとき(①の左辺)=2×1=2、(①の右辺)=1×(1＋1)=2より①は成り立つ
[２]n=k(k：自然数)のとき、①が成り立つと仮定すると
2(1＋2＋…＋k)=k(k＋1)…(※)が成り立つ
n=k＋1のとき、
(①の左辺)ー(①の右辺)
={2(1+2+…＋k＋k+1)}ー{(k+1)(k+1+1)}
={2(1+2+…＋k)}ー{k(k+1)}＋2(k+1)ー(k＋k＋1＋1)
={2(1+2+…＋k)}ー{k(k+1)}…②
(※)より、②＝０
よって、n=k＋1のときも①は成り立つ
[1][2]より、全ての自然数nで与えられた方程式は成り立つ[証明終]