【物理講師向け】2方向分解で斜方投射をわかりやすく指導しよう！

はじめに位置x, 速度V, 加速度a(一定)に関する3つの式を示します。

初めの位置を0,初速度Vo,時刻tとしておきます。加速度は速度の時間変化なので

V = Vo + at ・・・①

となります。

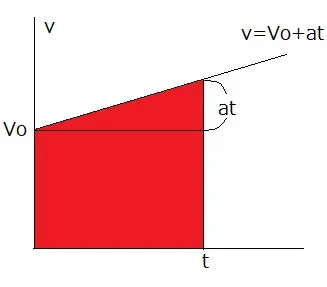
また、右図のような

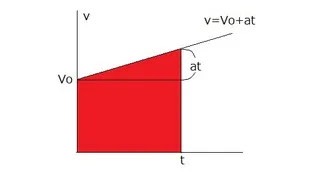
v-tグラフを考えると、図の赤い部分の面積が距離xを表します。そこで長方形部分がVot , 上の三角形部分が

   となることから、

      ・・・②

となります。

さらに、①と②からtを消去すると

       ・・・③が得られます。

この3つの公式は等加速度のときに成立する公式です。

ボールが最高点を迎える時間、地面に衝突する時間、そこまでの距離は？？

地面からθの角度の方向にボールをx=0,y=0の位置から初速度vで投げたとしましょう。このあと、ボールに加わる力は重力gだけとし、地面との衝突時の摩擦や減衰は考えないものとします。

水平方向

ボールに加わる力は重力のみなので水平方向には力は働きません。つまり、水平方向に関しては等速運動になります。今、地面と投げた方向のなす角がθであることから水平方向の初速度は v×cosθ となります。従って、時刻tでボールが進んだ距離はvcosθ×tとなります。

垂直方向

垂直方向には重力gが働いているので垂直方向に関しては等加速度運動になります。加速度a =-g です。初速度はvsinθなので時刻tにおけるボールの速度はvsinθ-gt となります。

さて、ここでボールが最初に最高点に達するときの時刻を考えてみましょう。ボールが最高点に達する瞬間は垂直方向の速度が0になるときです。従って、vsinθ-gt = 0 をみたすtが最高点に達するときの時刻です。従ってt = vsinθ/g となります.また、このとき、ボールは水平方向に関しては  

進んでいます。

次に、ボールが地面に到達する時刻を求めてみましょう。実はこれは簡単に求められます。ボールの軌道は放物線ですので、y=0から最高点に達するまでの時間と最高点からy=0に戻ってくるまでの時間は等しいのでボールが地面に到達する時刻は2vsinθ/g となります。

このように２方向に分解することで、力が全く働かない方向（水平方向）に関しては簡単な運動になりました。斜面上での運動時には運動方向とそれに垂直な方向に成分を分解すると楽になるときもあり、必ずしも地面を基準に考える必要はありません。

物理は上手な考え方を吸収する学問です。なかなか理解できない部分もあるかもしれませんが粘り強く頑張りましょう！！