【物理(力学)】入試問題の花形、二体問題！〜東工大の良問で攻略〜
物理の話をしているとよく出てくる言葉、二体問題。
これは文字通り２つの物体の挙動を扱う問題です。
２つの物体が接触して静止していたり、離れて異なる速度で動いていたり…
などなど多くの状態が考えられます。
今回はその中でも東工大の入試問題から、「摩擦の働く斜面上での2物体」について考えていきます。
この問題はいわゆる典型問題の良問なので、
二体問題の「力の成分表示」や「運動方程式の解き方」、「保存則」にいたるまで、
網羅的にマスターすることが出来ます。
この記事は物理の基本を一通り理解してはいるものの、
問題の解き方やその着眼点がわからない講師の方に向けているので、
そもそも運動方程式や運動量保存則がどのようなものであるかは理解しているものとして進みます。
また、一部簡単な積分を行う部分があるので注意してください。
それではまず、問題を解く前に、
力学の問題で用いるであろう公式とそれらを使うシチュエーションを列挙しておきます。
力学で用いる公式
①運動方程式
→時間tに関わる問題を解くのに用います。
②力のつりあいの式
→基本的には物体が静止している時に用います。
③エネルギー保存則
→時間tに関わらない問題を解くのに用います。
④(物体の運動エネルギー変化)=(物体がされた仕事)
→物体の移動距離や仕事に関わる問題を解くのに用います。
⑤運動量保存則
→弾性衝突時の速度を求めるのに用います。
⑥はね返り係数=1
→弾性衝突時の速度を求めるのに用います。
それでは以下で実際に問題に取りかかってみます。
問題文とその分析！
物理の入試問題を解く時はまず問題文に一通り目を通し、
それぞれの小問が受験者のどの能力を見極めようとしているのかを理解する必要があります。
例えば、この問いは「力のつりあい」を理解しているかを見極めようとしているな？
この問いはエネルギー保存則を上手く使えるかを見極めようとしているな？などです。
問題を解く前に、
どの問題にどの公式を用いるべきかを分析して理解していると問題を早く解けるようになります。
さて、以下が問題の全文です。
それぞれ問題文を読んだ際に問題文(赤文字の部分)から得られた分析結果(青文字の文)も載せてあるので、
確認してみてください。
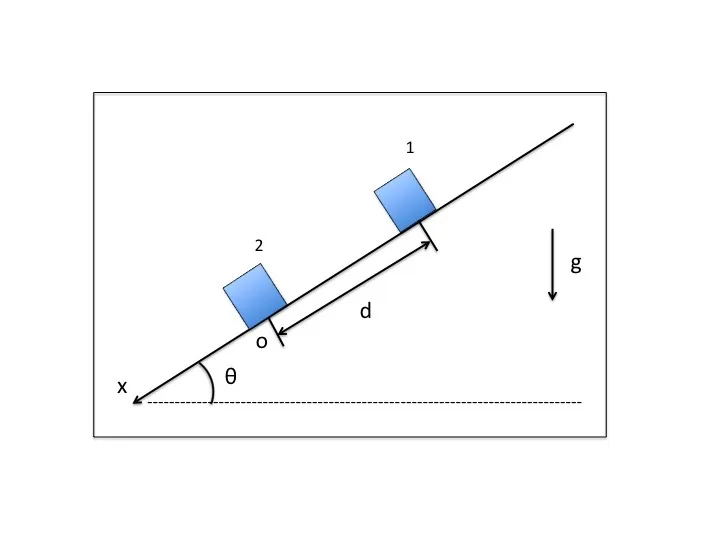
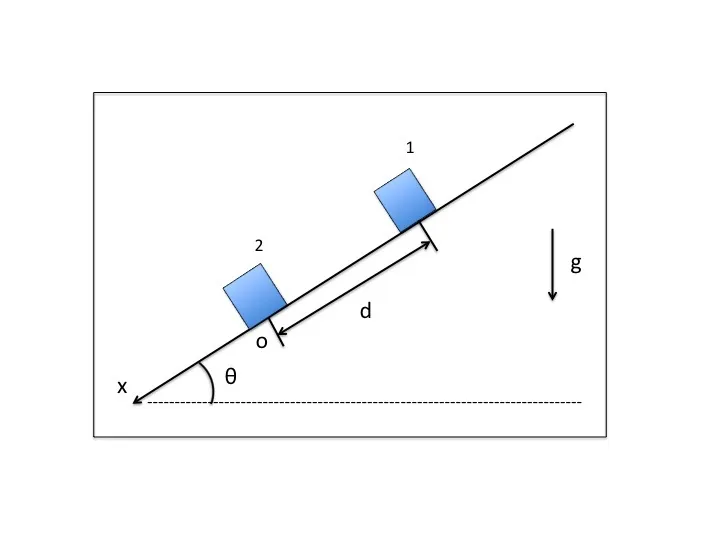
図のように大きさの無視できる質量m1,m2の物体1,2を水平面と角度θをなす斜面に沿って距離d離れた位置におく。
物体1と斜面との静止摩擦係数をμ1,動摩擦係数をμ'1、物体2と斜面との静止摩擦係数をμ2、動摩擦係数をμ'2とする。
ただし、m1<m2,μ1<μ2とする。
x軸を斜面に沿って下向きに取り、物体2の最初の位置を原点Oとする。
重力加速度をgとし、以下の問いに答えよ。
Ⅰはじめにd=0の場合を考え、物体1と物体2を密着し静止させておく。
角度θを0から変えていったところ、角度θoのとき物体1と2は同時に滑り出した。
(1)滑り出す直前の物体1と物体2の間の抗力の大きさをRとする。
滑り出す直前の状況において、物体1、物体2に働く力の斜面に平行な方向のつりあいの式をそれぞれ書け。
→力のつりあいの式を考えればよさそう。
(2)tanθoをμ1,μ2,m1,m2を用いて表せ。
→(1)で力のつりあいの式を求めているからその式を用いればよさそう。
Ⅱ以下、m1=m2=3m,μ1=μ'1=0の場合を考える。
斜面の角度をθとし、図のように物体1と物体2を距離d離れた位置に静かにおいたところ、物体2は静止したままで、物体1は初速度0で動き出し、物体2に完全弾性衝突した。衝突した時刻をt=0とする。
ただし、衝突は瞬間的に起こり、その際、摩擦力や重力の影響は無視できるものとする。
(1)衝突直前の物体1の速度v1と衝突直後の物体1,2のそれぞれの速度v'1,v'2をg,d,θを用いて表せ。
→衝突というワードから運動量保存則とはね返り係数=1の式を使えばよさそう。
(2)衝突後、物体2は動摩擦力により加速度が負の等加速度運動をした。
物体1との再衝突を考慮に入れない場合の、物体2が衝突後静止するまでの時間をt2とする。
また、物体1が衝突位置まで戻るのに要する時間をt1とするt2<t1が成り立つための条件をθ,μ'2を用いて表せ。
→t2<t1というワードからt2とt1を求めればよさそう。運動量保存則やエネルギー保存則では時間tは出てこないから時間tに関わるものを扱う運動方程式を解けばよさそう。また、物体が静止する時間にも着目するとよさそう。
(3)設問Ⅱ(2)の条件が満たされる場合を考える。t=0で物体1と2が衝突した後、再び衝突する時刻をt3とする。
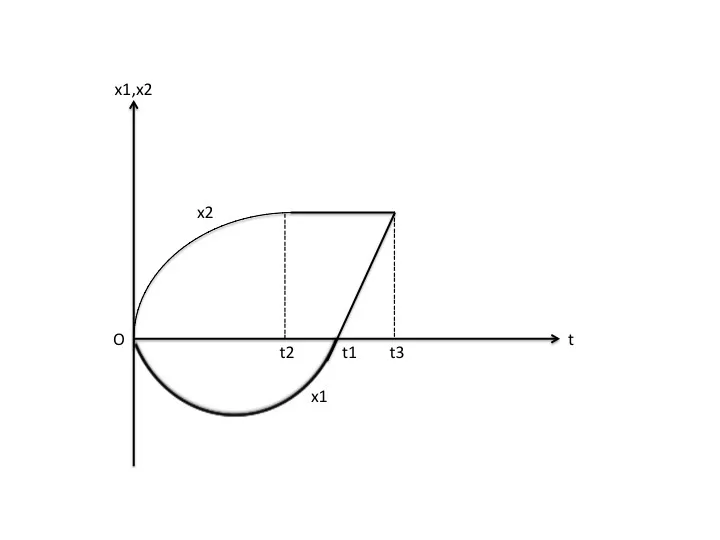
時刻0≦t≦t3について、横軸を時刻t、縦軸を物体1,2それぞれの位置x1,x2として、時刻変化の概略を表すグラフを描け。
ただし、縦軸の値をグラフ中に示す必要はない。
→グラフの概形を描くだけだからt=0,t1,t2,t3(物体の動きが変わる時刻)でのそれぞれの物体の位置x1,x2がわかればよさそう。
(4)設問Ⅱ(2)の条件が満たされる場合、物体1,2は衝突を繰り返し、そのたびに物体2は斜面を下り、衝突と次の衝突の間に物体1,2の離れる最大距離は減少していく。
最終的に物体1と2が一体となり静止するまでに物体2が斜面に沿って下る距離をθ,μ'2,dを用いて表せ。
→物体が静止する時刻がわかっていないから運動方程式は使えなさそう。物体の移動距離を求めるのだから(物体の運動エネルギー変化)=(物体がされた仕事)の公式が使えそう。
上記のように分析をして、
問題文のキーワードからどの公式を用いればよいか、どの公式は用いるべきではないか大体の見当を付けておくことが大切です。
それでは上記の分析を元に問題を解いていきます。
以下に問題のみの文面も載せてあるので是非使用してください！
問題文の分析に基づいた解答を見てみよう！
以下の解答の青字の部分は上記の分析と対応しています。
それを意識した上で解答を見てみてください。
Ⅰ(1)
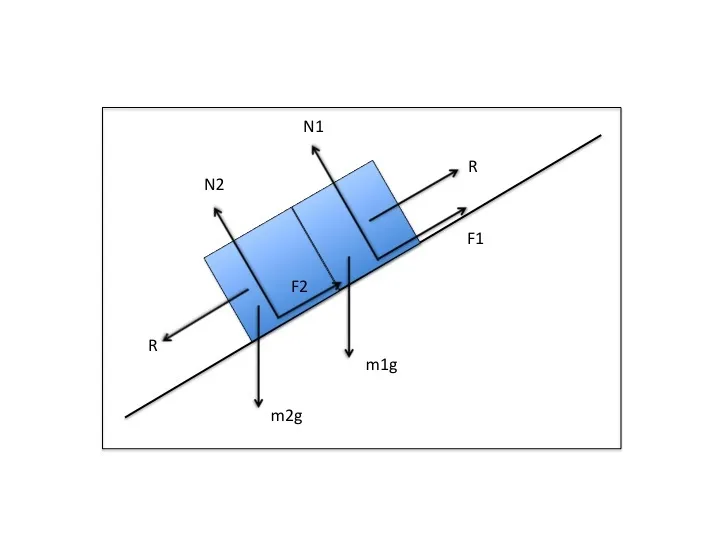
下図のようにそれぞれの物体に働く垂直抗力をN1,N2、最大静止摩擦力をF1,F2とする。
(最大静止摩擦力の定義より、F1=μ1N1, F2=μ2N2)
滑り出す直前は力のつりあいの式が成り立つ。
x軸に平行な方向とその方向に垂直な方向に分解して力のつりあいの式を考えると、
物体1,2のx軸に平行な方向
m1gsinθo−R−μ1N1=0, m2gsinθo+R−μ2N2=0
物体1,2のx軸に垂直な方向
N1=m1gcosθo, N2=m2gcosθo
これらから自分で定義したN1,N2を消去して、
m1gsinθo−R−μ1m1gcosθo=0, m2gsinθo+R−μ2m2gcosθo=0・・・①
(2)
①の２つの式からRを消去して解くと、
tanθo=(μ1m1+μ2m2)/(m1+m2)
Ⅱ(1)
運動量保存則とはね返り係数=1の公式より、
(運動量保存則) mv'1+3mv'2=mv1・・・②
(はね返り係数=1) (v'2ーv'1)/v1=1・・・③
これらだけでは式が足りない...分析が間違っていたのか？と思いきや！
力学で用いる公式③のエネルギー保存則を用いればv1が求まるんです！
物体1が動き出した瞬間と衝突直前のエネルギー保存則より、
mgdsinθ=(mv1^2)/2 ⇒ v1=√2gdsinθ・・・④
②〜④を解いて、
v'1=−(v1)/2=−(√2gdsinθ)/2・・・⑤
v'2=+(v1)/2=+(√2gdsinθ)/2・・・⑥
(2)衝突後の物体1,2の加速度をそれぞれa1,a2として、運動方程式を立てる。
m1a1=m1gsinθ→a1=gsinθ・・・⑦
m2a2=m2gsinθ−μ'2N2→a2=−(μ'2cosθ−sinθ)g・・・⑧
この元で物体1,2が静止する(速度が0)時に着目する。
まず⑤,⑥の両辺を時間tで積分して、
⑦→v1(t)=gtsinθ+v'1 (時刻tでの物体1の速度)・・・⑨
⑧→v2(t)=−(μ'2cosθ−sinθ)gt+v'2 (時刻tでの物体2の速度)・・・⑩
物体1の速度v1(t)が0になるのはt=(t1)/2(※参照)
物体2の速度v2(t)が0になるのは問題文よりt=t2。
※物体1が衝突後元の位置に戻るのにかかる時間はt1。
よって衝突後斜面上を駆け上がり最高点で静止するにはその半分の時間の(t1)/2だけかかる
以上を⑨,⑩に代入して⑤,⑥を用いて解くと、
t1=(v1)/gsinθ, t2=(v1)/2g(μ'2cosθ−sinθ)
t2<t1に代入して、
μ'2>3tanθ/2
(3)
t=t1に物体1が衝突位置(原点O)に戻るからx1=0
t=t2に物体2はある位置,x2=kで静止する。
t=t3に物体1がx1=kの位置で物体2に衝突する。
以上の点をプロットして、それらを曲線や直線で結ぶ(大体どう動くかは問題文を読めばわかる)と、
下図のようになる。
(4)
求める距離をLとする。
(２つの物体の最初から最後までの運動エネルギー変化)=(2つの物体にされた仕事)の公式を用いる。
２つの物体は共に最初と最後で静止しているからそのエネルギー変化は0。
２つの物体のされた仕事は重力のした仕事{m1gsinθ(d+L)+m2gsinθL}と摩擦力のした仕事{−μ'2m2gcosθL}の和。
よって、
0=m1gsinθ(d+L)+m2gsinθL−μ'2m2gcosθL より、
L=dsinθ/(3μ'2cosθ−4sinθ)
最後に！
皆さん、東工大の入試問題はいかがでしたか？
かなり難易度の高い問題ですが、各小問ごとにどの公式を使うかある程度見当を付けておけば、
それに従うだけでどの問題も解けてしまうので少しは楽になったかと思います。
次回は電磁気について扱います。
それまでにこの問題を何度も解き直して力学問題の解き方を頭に叩き込んでおいてくださいね！
