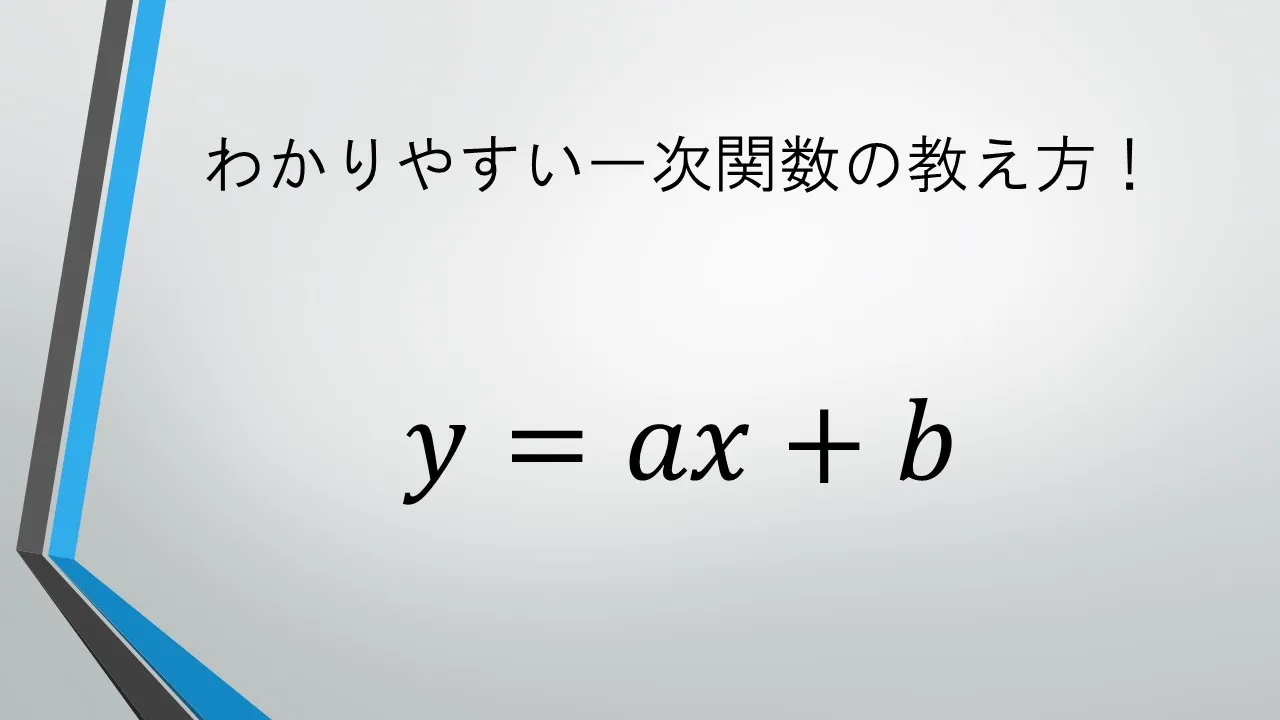
一次関数でつまづかせないために
一次関数は、比例反比例を学習した後にやってくる中学二年の数学の難所の一つです。この部分をしっかりと学習して理解できていないと、筆者自身がそうでしたがある問題が生じてしまいます。それは、
一次関数と一次方程式の違いがよく分からない、というものです。
講師の皆様方は当然ご理解の事と思いますが、生徒さんは中学校に入って初めて関数や方程式に触れます。違いを明確にしてあげないと、色々と大変な事になってしまいます。
筆者の以前見ていた生徒さんの中には、学習した当時、y=3x+4というような式を分からない、と言ってきた子がいました。聞くと、「xが求められない」と言うのです。当たり前ですね。慌てて違いを説明したのを覚えています。一次方程式を勉強して、「xとは求める数の事」だと思ってしまっていたのですね。
本稿では、
- 一次関数とは何かについて、一次方程式と比較しながら説明します
そして、
- どのような問題があるのかについてと、その解き方について述べていきます
一次と言うくらいですから、これは関数の基本です。これが出来なければ二次関数などはどうしても出来なくなってしまうでしょう。今後の数学を楽にするためにも、しっかりとした理解を築いていきましょう。
一次関数とは何か？
そもそも、「一次」とかついてはいますがこれは関数の問題です。
関数とは何なのかについての説明が先決でしょう。
関数とは、その漢字を見れば分かるように、
「数の関係」を表すものです。
とは言っても、別に「1+1=2」という式のイコールで結ばれているという関係性の様なものとは違います。
簡単に言ってしまうと、
「xにある数を掛けて、ある数を足すとyになる」というような関係の事です。
その上で、関数という言葉のルールとして、
「xの値が1つに決まるとyの値も1つに決まる」という知識にさせましょう。
一次関数と一次方程式の違いを分かってはいるもののどう説明したものか…という方もいらっしゃるでしょう。
まずは簡潔にその違いを述べてしまいましょう。これらは、求める物が異なります。
- 方程式では、未知の数xを
- 関数では、その関係性を
求めるのです。
あまりにも簡潔過ぎるので、もう少し詳しい分け方をしましょう。
一次方程式は、式の中に未知の数xがありました。xに正しくない数を当てはめようとすると、式が成立しなくなってしまうので、式が成立する未知数xの正体を求める、というものでした。
それに対して一次関数は、多くの場合「xが○だったらyは△である」というような条件が設定されています。それらの条件全てが成立する、「比例定数と切片」を求めるのが、一次関数です。勿論、そこから派生して通る点を求めたり、など求める物が多少変わる事がありますが、結果として行う事にはそこまで違いはありません。
そして更に、一次関数ならではの項目がありました。グラフです！ 式のx軸とy軸それぞれの数値の交点を通る、直線の形になりましたね。こちらも詳細はこの後記述しますが、基本だけ見ておきましょう。
さて、一次関数にも、基本の形となる式がありましたね。
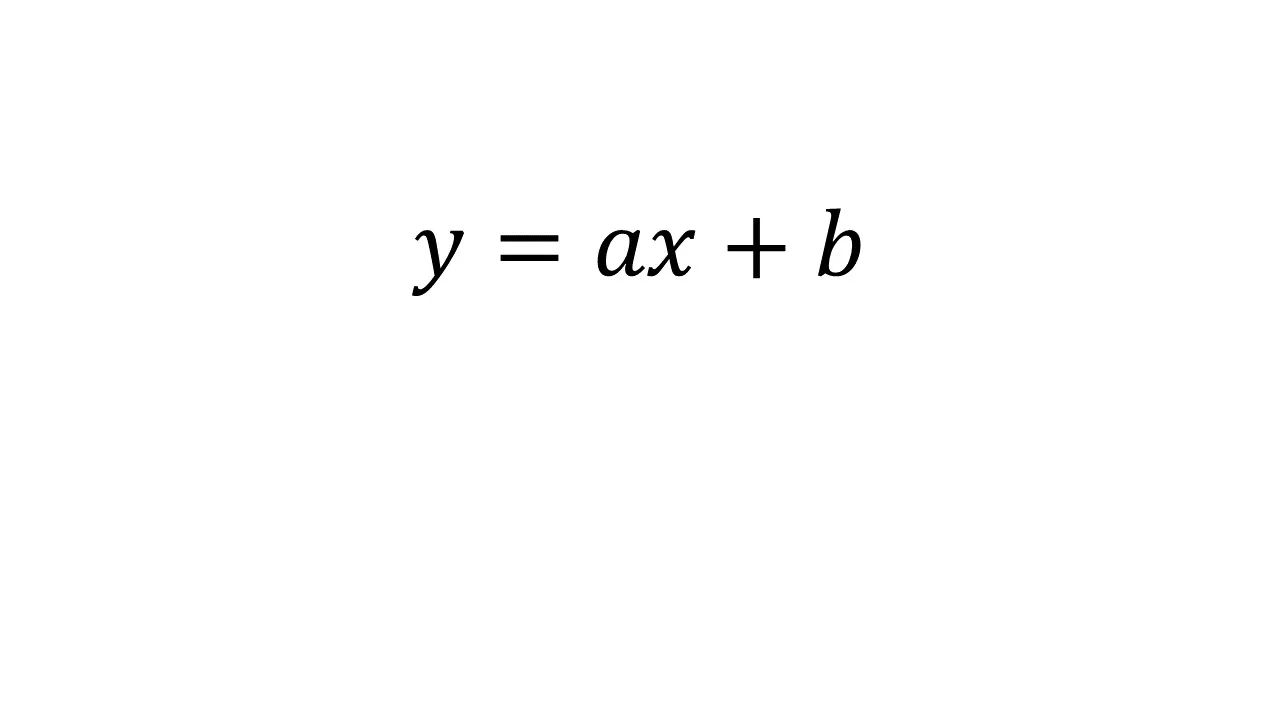です。先述の通り、「xにaを掛けて、bを足すとyになる」という関係性の式です。
aとbは定数であり、式の条件を満たす点を結ぶとそれがグラフになります。グラフについては特に、実際の問題を通して勉強するのが分かりやすいでしょうから、後に回しましょう。比例の式であるy＝axの式とほぼ同じである事、そしてグラフは比例の式と同様に直線であり、それが上下しているだけである事を初めに教えられると良いでしょう。
正直、生徒さんは口で言っても分かり辛いでしょうし、一次関数とは何かが分かったら、さくさくと問題に入っていきましょう。
問題の種類
さて、では一次関数の問題はどのようなものがあるのか見ていきましょう。このページで扱うのは。最も身近な、基本のパターンです。
どのような問題が出るのは分かっていただけたでしょうか。
- 「式を作りなさい」という問題
- 「グラフを作りなさい」という問題
- 「通る点を求めなさい」という問題
があります。
では、この4問をそれぞれ解いていきましょう。
問題の解き方
1問目
まずは先述の基本の式を出してみましょう。
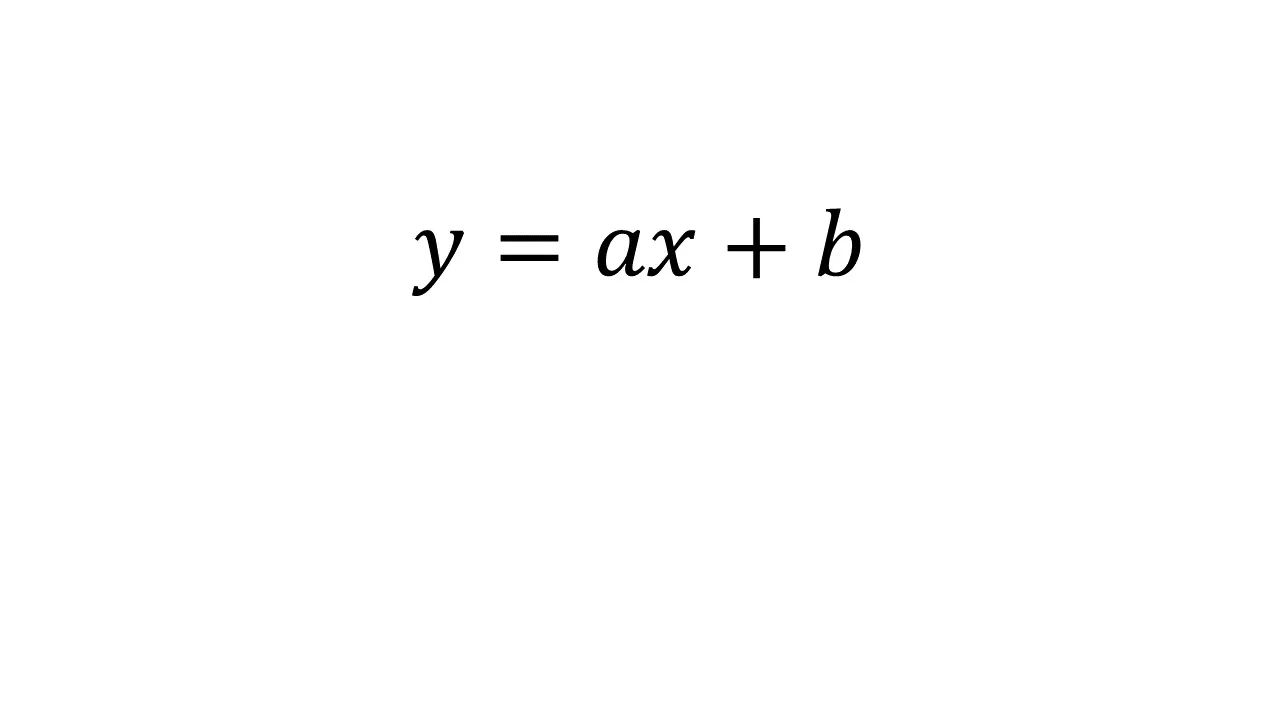
これに問題で与えられている値を代入してみましょう。
模範解答はこのようになります。
この解を出せたら、問題で与えられた数値通りになるかを確認する癖を付けておけると良いでしょう。
2問目
模範解答はこのようになります。1問目が理解できていればそんなに難しい事は無いはずです。同じように解いていける問題です。
3問目
いよいよグラフの問題のような意味合いを含んできましたが、これはグラフを書く必要はありません。
グラフの方が分かりやすい、という生徒には良いかもしれませんが基本的にグラフを書くのは時間がかかります。
可能ならばそうではない方法の方が良いでしょう。
まずは問題文を一般化します。つまり、
グラフ特有の（点、直線、など）の意味合いを除外していきましょう。
このように解答できるでしょう。
4問目
セオリーとしては3問目の前に学習する範囲ですが、ここではグラフとしてまとめるために最後に置きました。
まず解答から出してしまいますが、下図になります。
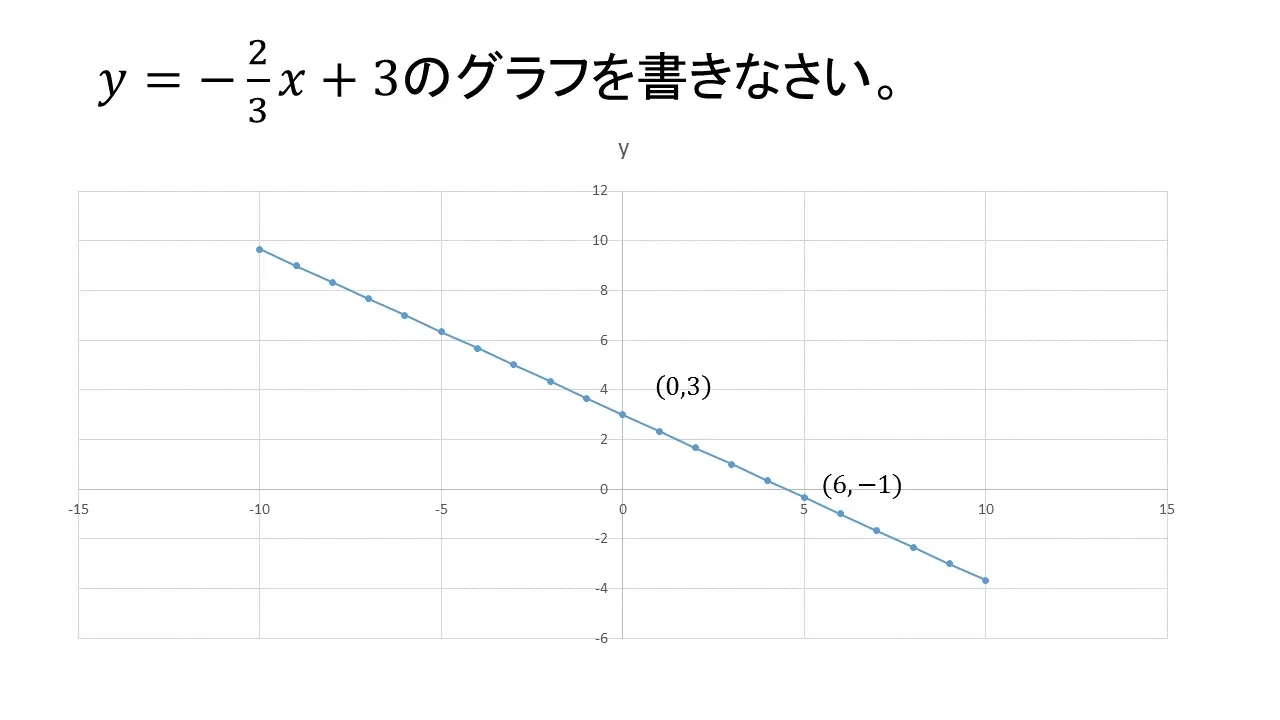
重要なポイントは、直線は二点が決まると一つのみに確定するということです。
式を使って二点を求め、その二点を通る直線を作れば完成です。
x方向に1進むと、y方向に比例定数ぶん増える（減少する）ことについて触れておけると、汎用性のある考え方が出来るようになると思います。
以上が、中学二年次に出て来る一次関数の基本的な問題とその解答方法でした。ここから応用問題に広がっていく大事な場面ですから、しっかりと様々なパターンに対応できるよう、盤石な理解を作ってあげる事が大切です。
運営部おすすめ記事
