これで完璧!【奇関数・偶関数】覚え方は?見分け方は?

奇関数・偶関数
これで完璧!覚え方は?見分け方は?
先日、カテキョ先の生徒から
偶関数と奇関数の定義が覚えられない
と相談されました。
この機会に筆者が受験生の頃に活用していた
偶関数と奇関数の覚え方を紹介します。
恐らく、このように覚えていた方も多いと思いますが…
偶関数と奇関数の定義
偶関数の定義
f(-x)=f(x)が成立するとき
f(x)は偶関数
特徴:y軸に関して対称なグラフ
例:y=cosx
奇関数の定義
f(-x)=-f(x)が成立するとき
f(x)は奇関数
特徴:原点に関して対称なグラフ
例:y=sinx, y=tanx
覚え方
グラフの形から理解する
偶関数、奇関数の式による定義よりも、
グラフの特徴を押さえることが重要です。
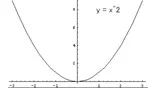
偶関数はy軸に関して対称なグラフなので、
xの2乗の関数も偶関数と言えます。
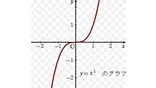
奇関数は減点対称のグラフなので、
xの3乗の関数も奇関数と言えます。
気付いている方も多いと思いますが、
xの偶数乗の関数=偶関数
xの奇数乗の関数=奇関数
と覚えましょう。
式を導く
グラフの形を押さえた後に、
関数の定義を自分で導き出しましょう。
次の式は偶関数か奇関数か確認しなさい
という問題を時々見かけます。
この際に、いちいちグラフを書くのは大変なので、式から判断できるように、
関係式を自分で導けるようにします。
偶関数の式
xの偶数乗の関数は、偶関数でy軸に関して対称と理解しました。
y軸対称ということは、
絶対値が同じ値を代入すると同じ値になるということです。
xの2乗の関数で確認します。

以上のようにして、偶関数の式が得られます。
※確認のためなので、ここでは数学的な正しさは問いません。
奇関数の式
xの奇数乗の関数は、
奇関数で原点に関して対称と理解しました。
今回も、絶対値が同じ値を代入して、関係を探ってみましょう。
xの3乗の関数で確認します。

以上のようにして、奇関数の式が得られます。
※確認のためなので、ここでは数学的な正しさは問いません。
まとめ
(1)xの指数が偶数だったら偶関数、奇数だったら奇関数
(2)y軸対称が偶関数、原点対称が奇関数であることの確認
(3)偶関数、奇関数の定義式を、xの偶数乗と奇数乗の関係から導き出す
(4)問題文に与えられている関数が定義式を満たしているかを考える
例:
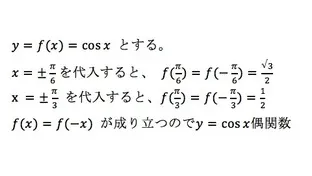
勿論、偶関数、奇関数の定義式がどっちがどっちかを覚えていれば十分なのですが、
こちらの方が、忘れにくいと思うので、使って下さいね!
算数・数学で人気の記事





![10円玉をピカピカにしよう!![高校化学]](https://www.juku.st/cdn/article_images/304/large_juku_entry_images_image.webp)