倍数変化算
以前、線分図の描き方と共に倍数算を紹介しましたが、今回は倍数算の応用の倍数変化算を扱います。
小学生の指導に慣れていない方は、馴染みが無い分野かもしれません…確認しておいて下さいね！
倍数算の復習
倍数算は、”一定なもの”をもとに立式します。具体的には、
片方が一定(誰か１人の量が変化せず一定)
A君は1800円、B君は1200円のお金を持っていましたが、A君がノートを1冊買ったので、A君とB君の残金の比が11：8になりました。ノート1冊の値段はいくらですか。(B君のお金が一定)
和が一定(合計の量が変化せず一定)
初め、姉と妹の所持金の比は3：2でしたが、姉が妹に60円あげたので、2人の所持金の比は5：4になりました。初めの姉の所持金はいくらでしたか。(所持金の合計が一定)
差が一定(差の量が変化せず一定)
姉は5000円、妹は4500円持っていました。姉と妹が同じ金額を出し合ってプレゼントを買ったら、姉の残金は妹の残金の3倍になりました。2人が買ったプレゼントはいくらでしたか。(所持金の差が一定)
の３つのパターンがあります。
倍数変化算とは
倍数変化算は、倍数算では対応できないときに利用します。”一定なもの”が無い場合に用いると覚えて下さい。
例えば、
兄と弟の所持金の比は3：1でしたが、おじさんから兄は800円、弟は400円もらったので、兄と弟の所持金の比が7：3になりました。はじめに兄はいくら持っていましたか。
これは、先ほどの倍数算の３つのパターンに当てはまりません。
こんな時に登場するのが倍数比例算です！！
倍数変化算
では実際に解法に入って行きます！！
解き方の手順
① 比例式をつくる
② 内項と外項の積を計算する
③ ②で分配法則を用いる
④ 「＝」イコールの左右の数値の差をとる。
①できちんと式を立てられれば、②～④は単なる計算です。
内項と外項の積が等しくなることは、実際の比例式と共に確認しておくと良いでしょう。
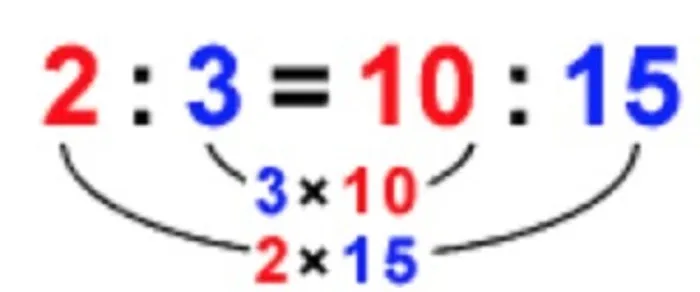
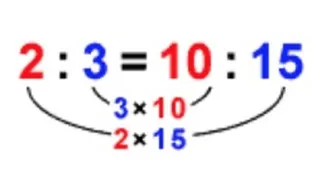
たとえば，２：３＝10：15という比例式がなりたちますが、 同時に外項の積（２×１５）＝内項の積（３×１０）も成り立っています。
式の立て方&解法
<問題>
兄と弟の所持金の比は3：1でしたが、おじさんから兄は800円、弟は400円もらったので、兄と弟の所持金の比が7：3になりました。はじめに兄はいくら持っていましたか。
<解答>
兄と弟の最初の所持金の比が3:1だったので、兄の所持金を③、弟の所持金を①とおく。
おじさんからお金をもらった後の所持金は、
兄は、③＋800(円)
弟は、①＋400(円)
になります。それが、7:3なので、
(③＋800)：(①＋400) ＝ 7:3
先ほどの内項と外項の積の関係を用いると、
3×(③＋800) = 7× (①＋400) なので、
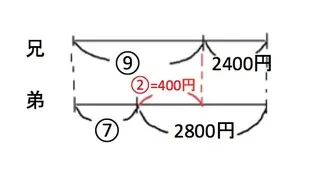
⑨＋2400 = ⑦＋2800 (★)
⑨ー⑦ ＝ 2800-2400
②=400
①=200
よって、兄の最初の所持金は③なので、200×３＝600円になります。
式変形が苦手な生徒さんには、(★)以降は、線分図で説明して下さい。
