塾講師のみなさんはベストな方法を指導できますか？円錐の体積、表面積の求め方！

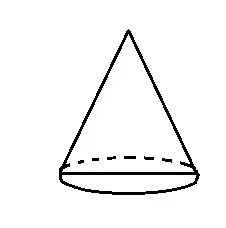
右図のような円錐を考えます。

底面の半径を3, 母線の長さを5とします。中学3年生で習う三平方の定理を習えば、これだけの情報で円錐の体積を求めることができますが、ここでは中学1年生向けとして高さを4としておきます。中学3年生にはどこに三平方の定理を用いることで高さを求めることができるのか考えさせるのもいいかもしれませんね。

 

体積を求める

体積を求める方法は一通りなので簡単に紹介します。

錐体の体積：底面積×高さ×1/3  です。

三角形の面積は　底辺×高さ×1/2 　と求めていたので、1/2 と1/3を混同する可能性が考えられます。平方センチメートル、立法センチメートルのcmの肩につける数字と同じ！

と関連付けて教えるといいかもしれませんね。

表面積を求める

表面積を求めるときには　展開図をつかう　です。頭の中だけで表面積を考えようとすると見落とす危険性があるので展開図を書かせる習慣をつけさせるべきです。展開図は右図のようになります。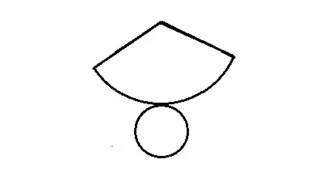

円錐の表面積で生徒が迷うポイントは　

側面の扇形の中心角が一目では分からない

です。扇形の面積を求める公式は円の面積に中心角/360°をかけて求めることが一般的です。したがって、中心角が必要になります。ここをどう解決するか3つの方法を紹介します。

①扇形の弧の長さ＝底面の円周　を用いる

扇形の中心角をx°としておきます。そうすると、扇形の弧の長さは2×5×π×x/360

となります。底面の円周の長さは2×3×πとなります。この2つを=で結び、xの一次方程式として解くと、x=216°　となります。あとは扇形の公式に沿って側面積を計算し、底面積(9π)を加えることで三角錐の表面積が24π　と求められます。

• 長所：本質を捉えており、中心角が分かっていて、母線の長さが分からない時にも対応できる。また、一次方程式の気分で解ける。
• 短所：解答が長くなるので、ちゃんと説明しないと生徒に難しいという印象を与えてしまう恐れがある。また、書くのに時間がかかる。

 

②中心角/360°　は、底面の半径/母線　と覚えさせる。

これは①で=で結んだ式　

2×5×π×x/360 = 2×3×π

の両辺からそれぞれ2πを割り、左辺をx/360 にすれば右辺は3/5 となり、底面の半径/母線　となることから導き出せます。これを使えば側面積は25π×3/5 = 15π　となります。

• 長所：360など大きな数が出ることもなく、計算の手間が省ける。「母線分の半径」など簡単に覚えられる。母線が分からなくて中心角が分かっているときでも対応できる。
• 短所：なぜx/360 = 底面の半径/母線　なのか理解しない可能性がある。

③扇形の面積を求める公式：lr×1/2 (l:扇形の弧の長さ、r:母線) を使う。

円錐の場合、扇形の弧の長さは底面の円周の長さに等しい。なぜなら

であるからです。側面積は1/2 ×(3×2×π) ×5 = 15πとなります。

• 長所：計算が簡単に済む。さらにlr×1/2はよく知られた公式なので、記述式でも減点されにくい。さらに、このlr×1/2 は円錐絡みの問題で有効に働くことが多い。
• 短所：lr×1/2 のrを底面の半径と勘違いする可能性がある。中心角が分かっていて、母線の長さが分からない時に対応できない。

①～③まで様々なメリット・デメリットがありますが、生徒のレベル、時間などを考慮してどれを教えていくか考えてみてください。

 

 塾講師ステーションTOPへ戻る

運営部おすすめ記事

すぐにアルバイトを始めたいあなたにオススメ。

 

理系のあなたに！国語ってどうして勉強するか知ってますか？

【塾講師必見】国語の教え方はこれだ！そもそも国語って何を教えるの？

 

塾講師バイトの時給が気になる!!~平均月収はいくら!?~

 

【塾講師バイト必見！】生徒への接し方はこれだ！

 

 塾講師ステーションTOPへ戻る