公開日 2014/06/12
更新日 2026/01/20
【算数講師必見】必須テクニック！つるかめ算を小学生に指導しよう！
面積図を用いてつるかめ算を解こう！
小学校算数の代表とも言えるつるかめ算を扱います。中学生になると方程式を使うことでさっさと解けてしまうので、方程式に慣れていると逆に教えるのが難しいですよね。今回は定番ですが面積図を用いた解法について解説していきます。
つるかめ算とは？
つるかめ算は、つるとかめのように異なる足の数を持つ動物の数の合計と足の数の合計が分かっているときに、それぞれの動物の数を求める算数です。実際に問題を扱ってみましょう。
例題：つるとかめが合わせて15頭います。足の数の合計は40本です。つるとかめは、それぞれ何匹いるでしょうか？
面積図
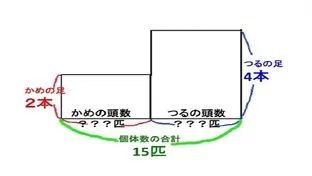
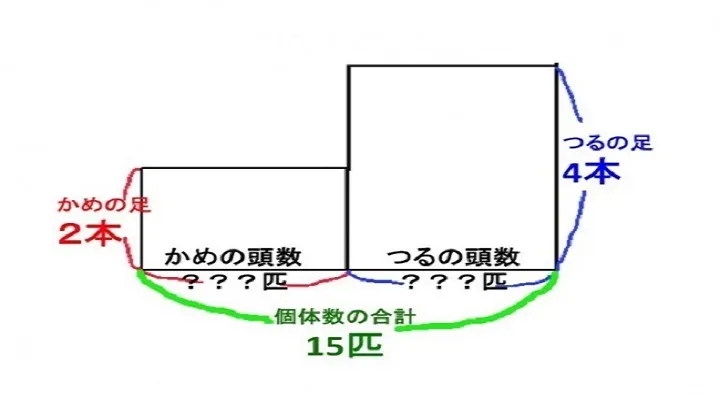
つるの足の数は2本、かめの足の数は4本です。
面積図を書いていきます。つるとかめそれぞれに対し長方形の面積図を書きます。
縦に足の数、横に頭数を書きます。←ポイント
”頭数の合計が分かっていること”をうまく使って行きます。
面積図が書けるとあとは面積の問題として扱うことができます
与えられた足の数の合計(40本)は、２つの長方形の面積の合計です。
計算の仕方
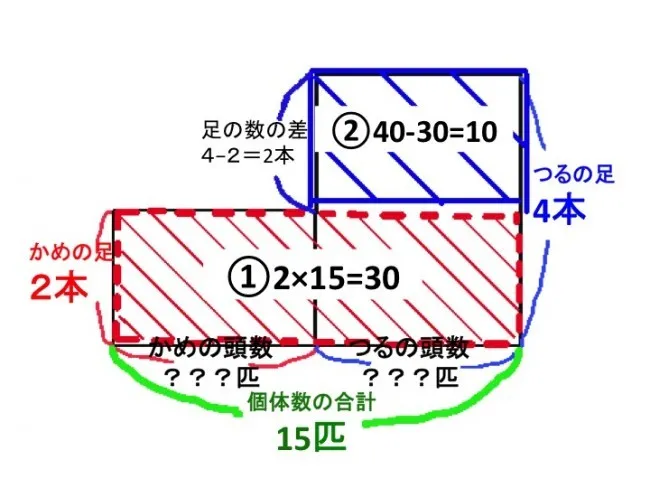
では、実際に計算していきます。縦に２つ並んでいた長方形を別の分け方をすることで、求められる面積から求めて行きます。
①2×15=30 (赤斜線部の面積)
②40-30=10 (青斜線部の面積)
②まで出せたら次に足の数の差に着目します。足の数の差は2本ですね。
面積が10(青斜線部)で縦の長さが2の長方形なので、横の長さは10÷2＝5 (頭) これがつるの個体数になります。
かめの個体数は15-5＝10 (頭)
