平方完成の意味を直感的に理解すること
本記事の指導対象学年：高校1年生
中学校では2次関数の基本的な形を学びます．すなわち，頂点の座標が原点であるタイプの2次関数のグラフです．
そして，２次関数は高校の学習範囲になると，頂点の位置が変わります．そして，2次関数のグラフを書くために初めて平方完成というものを学びます．
この記事では前回の記事である
【関数のグラフに関する指導の要点まとめ～基本の“き”～】
URL:http://www.juku.st/info/entry/1122
でもふれた平行移動と対称移動という概念を使って,高校生に2次関数のグラフについてわかり易く説明する方法に関する指導方法について書いていきたいと思います．
今回の記事の目標
今回の記事では2次関数の平方完成と，その意味を理解して,グラフとして書けるように指導することを目的としています．
生徒には最初に以下の2次関数のグラフが書けることであると明示してしまいましょう．
数式の変形にも目的と意味があることを,私は指導の際に強調して生徒に伝えることにしています．
この理由はまたどこか別の記事で書きたいと思いますが,それを前提として，目標は上記のグラフを平方完成して書けることと，その意味を理解することとして記事を書いていきます．
関数の基本形
関数には基本となる形：基本形というものがあります．
初めに基本形ついて触れたいと思います．例えば,前回の記事で例として扱った1次関数や今回の記事でフォーカスしている2次関数では以下のようになります．
1次関数の基本形とそのグラフ
- 基本形
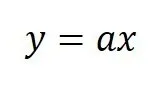
- グラフ
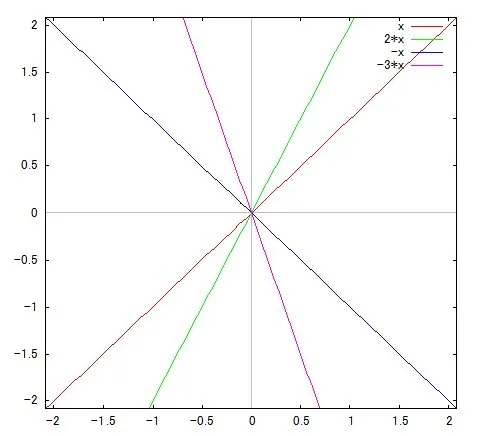
上記のグラフはaの値を変えることで，グラフがどうなるかを示してみました．
1次関数は上記のように，ａを変えるとグラフがどのように変わっていくことを生徒に最初に伝えます．
2次関数の基本形
1次関数の基本形について復習をしましたので,次に2次関数について導入を行います．2次関数の基本形は中学校で学ぶ範囲ですので，そんなに長く時間をとる必要はありませんが，導入としてもっとも簡単な2次関数を例に授業を展開します．
- 基本形
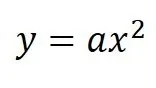
- グラフ
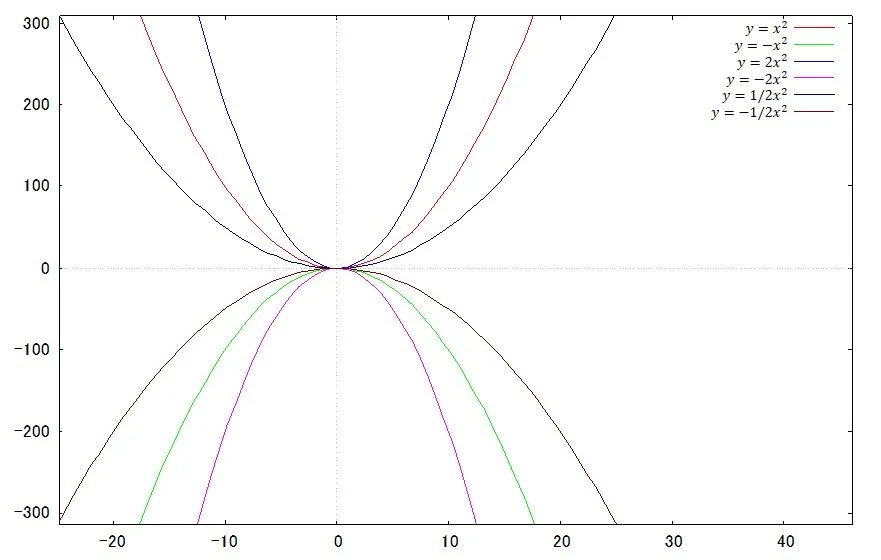
さて，今後の記事でもこの基本形については必ずと言っていいほど触れていきます．様々な関数を指導する際にポイントとなるのはこの基本形であると私は考えているからです．さらに言えば，その関数の大切な特徴を指導するのに必須な要素が込められているからです．
2次関数の基本的なグラフ
さて，上記でも書きました通り,2次関数の基本形とグラフは以下のようになります．
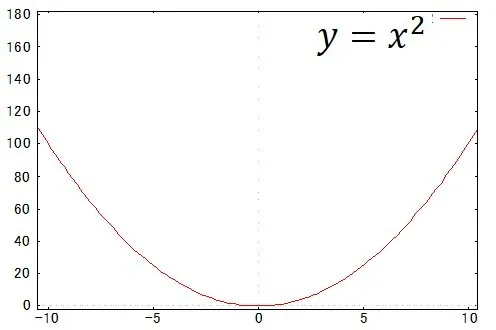
2次関数の形はすべて基本的には同じ形をしています．
2次関数の形，もう少し直感的な言い方をしますと，グラフの開き方はaの大きさを変えることで変わります．
aの正負を入れ替えると上に凸と下に凸というグラフの形が変わります．例えば以下のようにです．
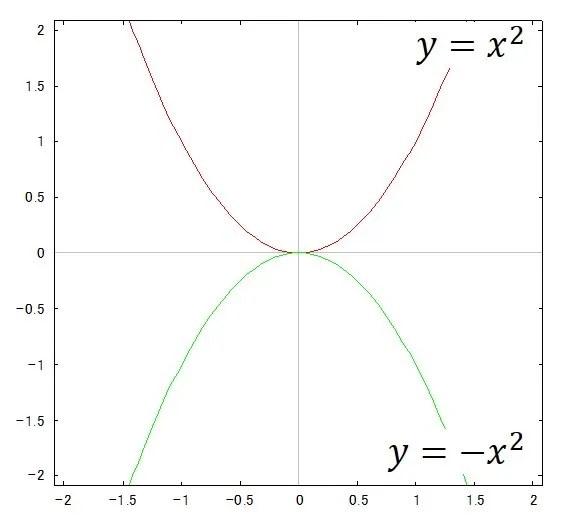
ですので，aはグラフの形を決定する重要なパラメータであることをしっかり生徒には伝えていきましょう．
2次関数のグラフの意味
また，基本的には同じ形と述べましたが，2次関数の形の意味について直感的に話してあげると，2次関数を身近に感じてもらえるかと思います．
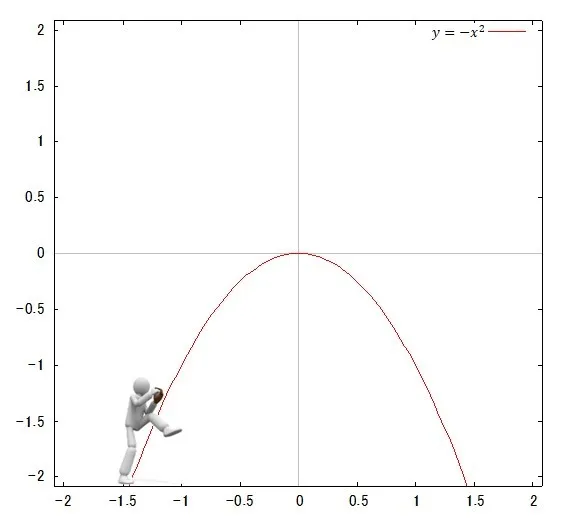
2次関数は放物線といいますが，物を放ったときの軌跡を表す線であることを意味します．
この意味で分かりやすいグラフは以下のように上に凸のグラフのほうが自然に思えますね．
平方完成とグラフの移動
平方完成の目的
平方完成の具体的な方法について指導する前に，次のことを生徒にはしっかりと伝えることが大切です．
- なぜ平方完成をする必要があるのか．
目的を明示しないままに数式の変形を示すことは，生徒にとっては今，自分が何をしているのかも分からず，板書を写すだけの時間になってしまいかねません．
では，平方完成の目的と言われて，生徒にわかり易く伝えるにはどうすればよいのでしょうか？
それは次の一言でいうことができます．
- 頂点の座標を明示すること
平方完成と頂点の関係
ここで，2次関数の頂点は以下の図（黒点）に示す通りです．
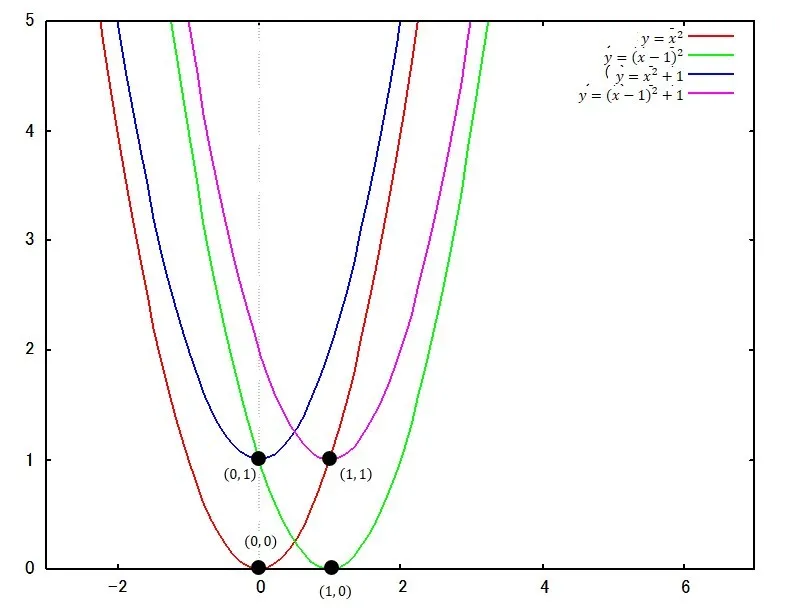
上記の2次関数はaの値は４つとも１である関数ですので，下に凸のグラフを示しており，グラフの開き具合は同じです．いずれも頂点の座標のみが異なる2次関数を表しています．
2次関数の頂点Aの座標を
とした時，2次関数は以下の式で書くことができます．
平方完成の基本事項
生徒に平方完成の目的を示したら，平方完成の具体的な方法を指導していきます．
この時のコツはいきなり一般的な形から指導しないことです．
具体的な例を挙げて，それに照らし合わせて，一般形を並べて記述しましょう．
扱っている教材や学校の教科書の例を使うのが良いです．
ここでは簡単でわかり易い2次関数の一例として，以下を例に解説をしていきたいと思います．
この2次関数を平方完成する手順を説明します．
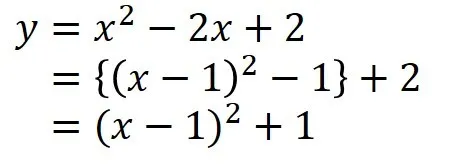
そして，次に一般形の説明に入っていくと良いでしょう．
2次関数と平行移動，対称移動の関係
平行移動
上記で平方完成で２次関数のグラフを書く方法について提示しました．
次に平方完成によって得られた式の意味について示したいと思います．
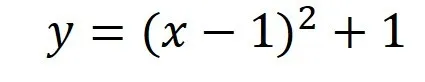
この形を変形して次のように置き換えてみます．
さて，このように考えると平方完成の意味するところが分かってくるかと思います．
2次関数のもっとも単純な形は以下の通りです．
この形のｘとｙを以下のように置き換えると，平行移動を意味していることが分かってきます．
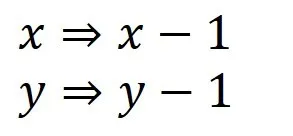
1次関数の場合と比較してみましょう．
1次関数の平行移動は次のようにかけたかと思います．
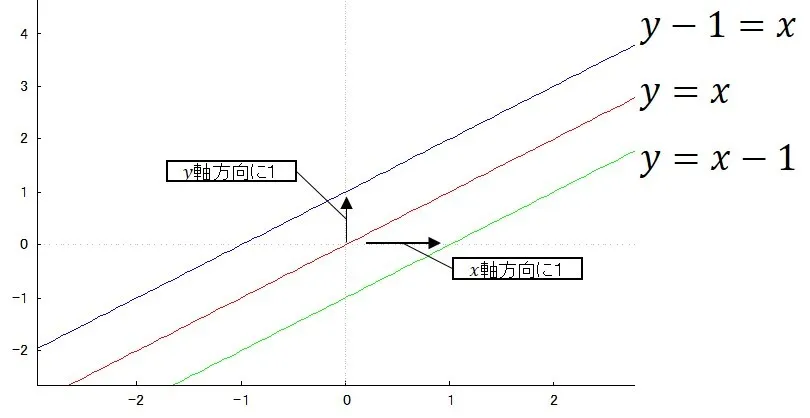
一方，２次関数は以下のようになります．
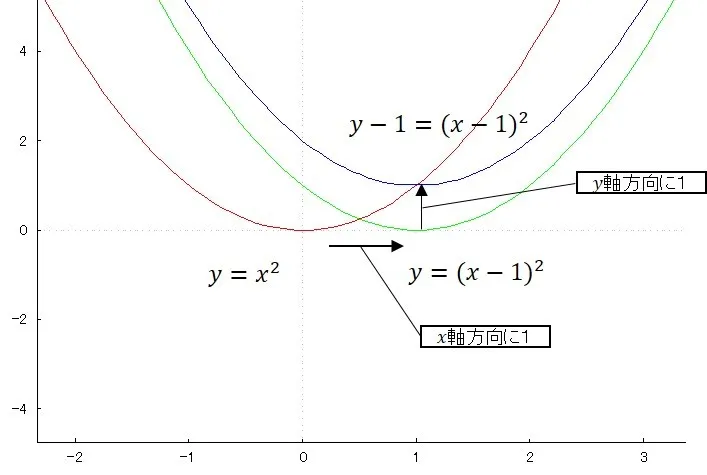
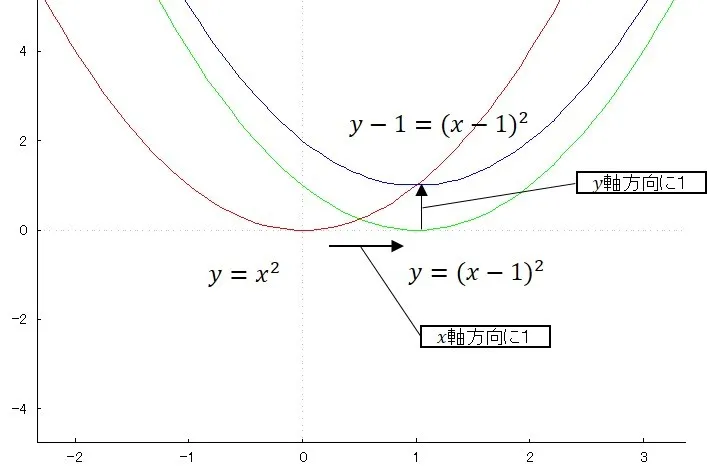
x軸方向に１，y軸方向に１平行移動した関数と，先の平方完成の例に挙げた２次関数は同じグラフであることが分かるかと思います．
このように,平行移動と2次関数の平方完成がつながります．
2次関数の基本の形，すなわち放物線を保ったまま，平行移動していくと，様々なグラフが書けることになります．
続いて対象移動と2次関数のグラフについてです．
対象移動
2次関数のグラフの形は大きく分けて2種類に分けられます．すなわち，以下の2つです．
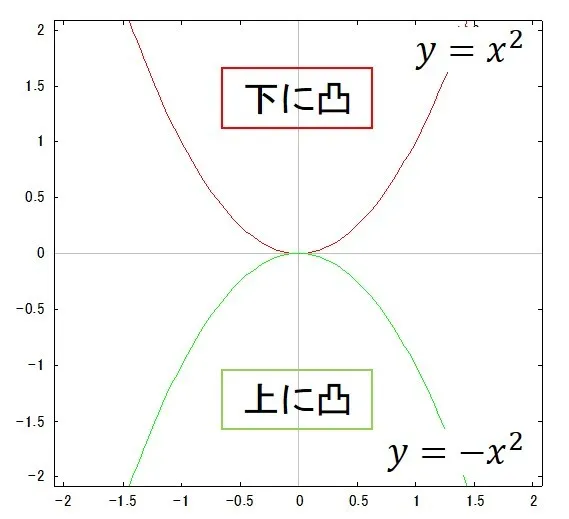
上に凸か下に凸かを決めるのはａの値が正なのか，負なのかに依存していました．
しかし，見方を変えれば，ｙの正負を入れ替える対象移動とみることもできます．
x軸に関する関数対象移動を行うと2次関数のグラフは上に凸，下に凸という見方をすることができます．
y軸に関する対称移動は前回の記事でも書きました通り，以下のようになります．
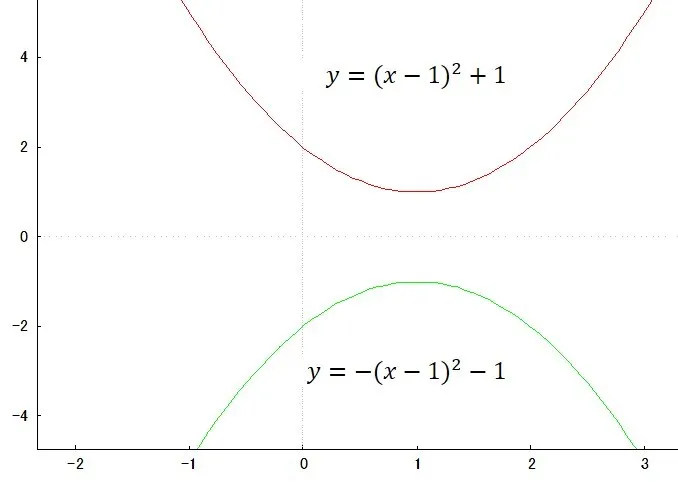
上の赤い２次関数を対象移動した結果が下の緑の２次関数です．
そのことを数式で書いてみましょう．
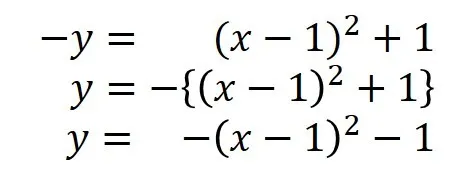
この式は
をx軸方向に１，y軸方向に-1平行移動した式とも見ることができます．
まとめ
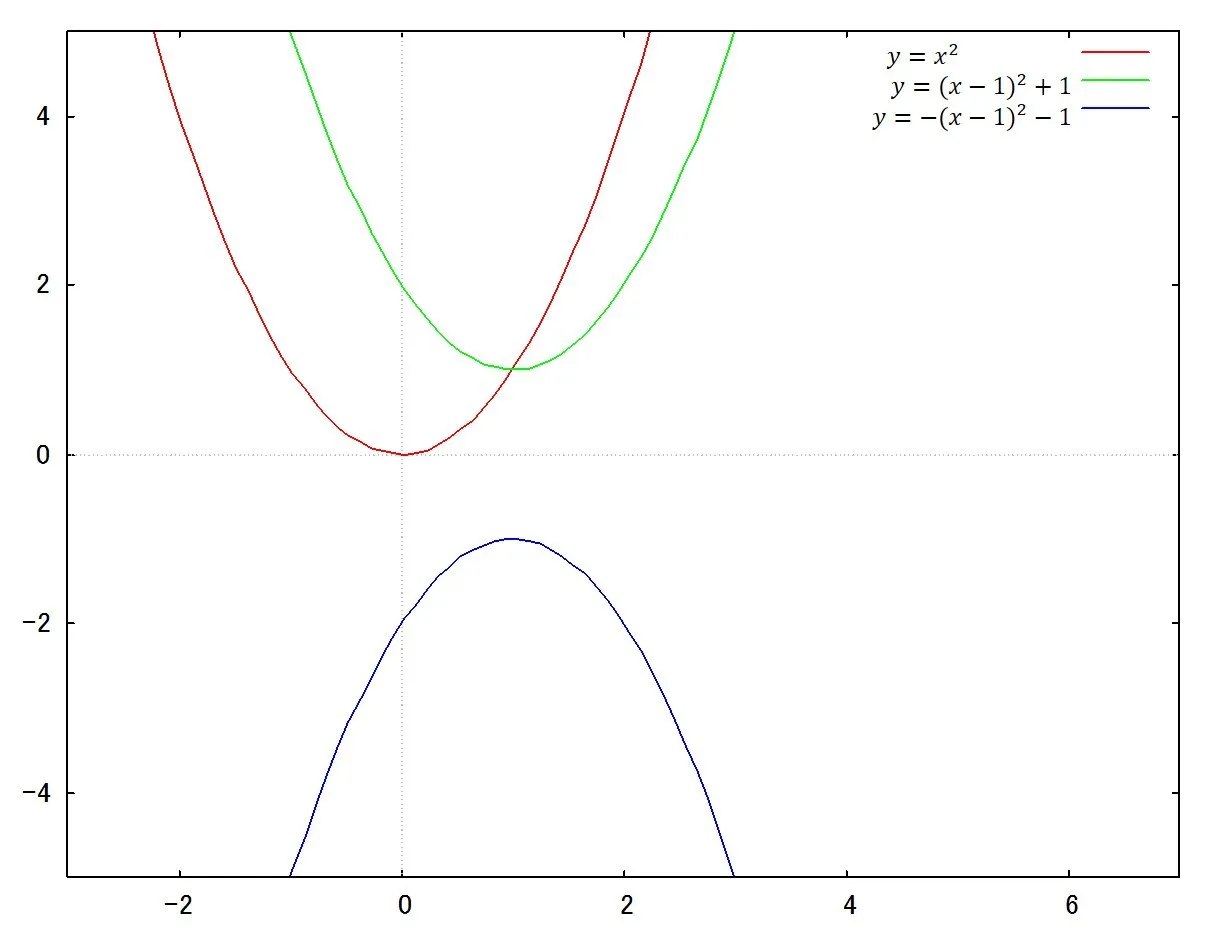
以上で，以下のグラフを示したことになります．
平方完成で得られる形はいずれも基本の形である以下の2次関数を対象移動と平行移動した形で書けることをここまでで解説しました．
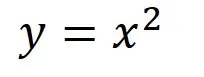
平方完成の結果はグラフの移動である．
このことを伝えられると，少しは平方完成に親しみを持ってもらえるのではないでしょうか．
