公開日 2014/06/14
更新日 2026/01/20
センター数学|恒等式を判別する分かりやすい方法！
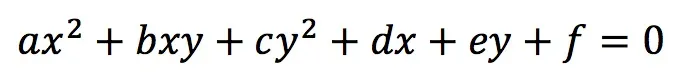
今回は数Ⅱで学習する恒等式に関する指導法を紹介します。教科書ではさらっと扱われているために、忘れてしまう方も多いと思います。
恒等式の基礎をきちんと押さえながら進めていきましょう。
以上が、青チャートに載っている基本事項の引用です。しかし、この知識だけでは使いにくいですよね。
まず、恒等式のイメージをつかむために、次の問題を説明していきましょう。
(式1)を見てみましょう。
- x=0のとき(左辺)=(右辺)=0
- x=1のとき(左辺)=(右辺)=4
- x=2のとき(左辺)=(右辺)=10
（左辺),(右辺)ともに2次式ですが、3個以上の異なるxの値について成立するので恒等式です。
(式2)を見てみましょう。
- x=-1のとき(左辺)=(右辺)=3
- x=3のとき(左辺)=(右辺)=-1
上記以外に(左辺)=(右辺)を満たすxの値はありません。よって、2次式で2個のxの値についてのみ成立するので恒等式ではありません。
恒等式は”どんな実数xを代入しても成立する式”ということです。「恒常的」に「等しい」「式」と書いて「恒等式」ですので、「常に等しい式」という意味になります。
それまでは、（式2)のように、「n次の方程式はn個の実数解を持つ」と学習してきたかと思います。
しかし、n次の恒等式はn+1個以上のxについて成り立ちます。つまりどんな実数xを代入しても成り立つということです。
もっと端的に言うと、(右辺)を（左辺)に移動させて、xを求める時に、xが求められたら(x＝－１,3のように、決まった解が出せたら)それは恒等式ではありません。
以上の前提によって、<２つ以上の文字の恒等式とその係数>の事項を確認します。
xとyの恒等式ということは”どんな実数x,yを代入しても成立する式"ということです。どんな実数を代入しても等式を成立させなければならないということです。よって
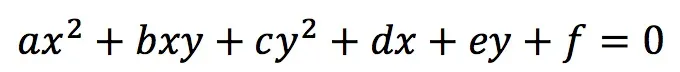
が常に成り立つためには、係数a=b=c=d=e=f=0が必要になることが分かります。
