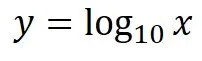
対数関数は指数関数の逆関数！しっかり意味を理解させよう
本記事の指導対象学年：高校２年生
関数のグラフに関する指導の要点まとめシリーズの第５回である本記事では対数関数に絞って執筆していきたいと思います．
高校２年生にして， logという新たな数学記号が登場しますね．logをイメージしづらい生徒もいることでしょう．
この記事ではlogに関して指導する際のポイントと，グラフに関して述べたいと思います．
特にlogの指導に関してのコツを最初に一言伝えておきます．
数学が苦手な生徒には特に具体例を示して比較して教えていくことがポイントです．
では,そのうえで具体的な指導法について書いていきたいと思います．
指数の復習
対数は指数とは切っても切れない関係にあります．そのためにも，授業の冒頭で指数の基本的なことを,復習および確認しておく必要があると私は考えています．
ですので，簡単に冒頭，以下のように指数は何であったのかを復習しておくと良いかと思います．
そのうえで，対数の説明に移っていきましょう．
対数とは何か
対数は何を計算しているのか？このことを説明するために，掛け算と割り算の対比を紹介してみます．
- ２×３＝６ ２を3回足したら６
- ６÷２＝３ ２を何回足したら６？
割り算は掛け算とはある意味，逆の計算でした．
指数と対数も同様の関係にある
このことを直感的に話してしまいましょう．そのうえで以下の例を紹介してみます．
このように，指数は２を3回かけるという計算ですが，log８は２を何回かけた結果であるかを計算する関数です．
すなわち，関数の初回の記事でも書いたように,こういう機能なのだと説明してしまいましょう．
ですから，以下のような書き方もできるということをここで話しても良いかもしれません．
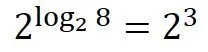
このように授業の初めに具体例を示したら，一般的な基本形を話していきます．
対数法則
以上の説明をしたうえで対数法則の説明をするとよいですね．
対数法則は以下のものでした．
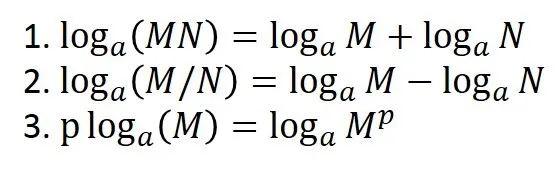
対数法則を指導する際のコツですが，ａ＝２，M＝２，N=４というような具体例を示してみましょう．
このように具体例を見せることが対数法則を直感的に理解してもらうためのコツであるかと思います．
１．と２．に関してですが，そもそもlogは全体で指数を表しています．このことを考えると，指数の部分を足したり引いたりすることはかけたり，割ったりすることに相当することが直感的にわかるかと思います．
３．も同様ですね．
対数関数は桁数がわかる
では，対数関数は何に利用されるのでしょうか？
このことを生徒に伝えておかないと，「指数関数の逆！なんだ！簡単じゃないか！」で終わってしまいます．
対数関数にはとても便利な使い方があります．
それは桁数がわかるということです．以下の例を紹介してみましょう．
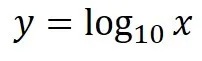
このlog関数のｘに１を入力してみます．
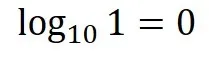
１は何桁の数字ですか？１桁ですね．
０に１を足すと桁数になりました．
続いてｘに10000を入力してみます．
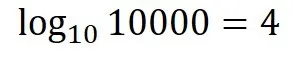
10000は何桁の数字ですか？5桁ですね．
４に１を足すと桁数になりました．
このように底が10のlog関数を考えるとその数字が何桁であるかがわかりますね．
もちろん，99のような数の桁数もわかります．
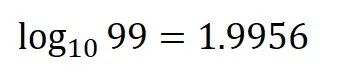
小数点以下を切り捨てて１を足したら２になるので99は２ケタであることがわかりますね．
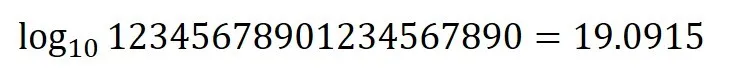
このようにすぐに何桁かわからない数字でもlogを使えば20桁であるとすぐにわかりますね．
logは桁数を知るのにとても便利なのです．
基本形とグラフ
基本形
logの基本形の話に移ります．
logの基本形は以下の通りです．
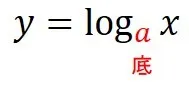
ここで，生徒にはこの関数の意味を理解しているか式の意味を日本語で説明できるかを聞いてみましょう．
ａのｙ乗はｘ
こう答えられれば，まずは問題ないでしょう．
このことを説明できるかどうかは，対数に関する問題を解く際にもポイントとなってきます．
このことはしっかりと生徒に理解してもらえるように説明をしていきましょう．
グラフ
さて，基本形に関して説明をしてきました．
次にグラフの説明をしていきます．
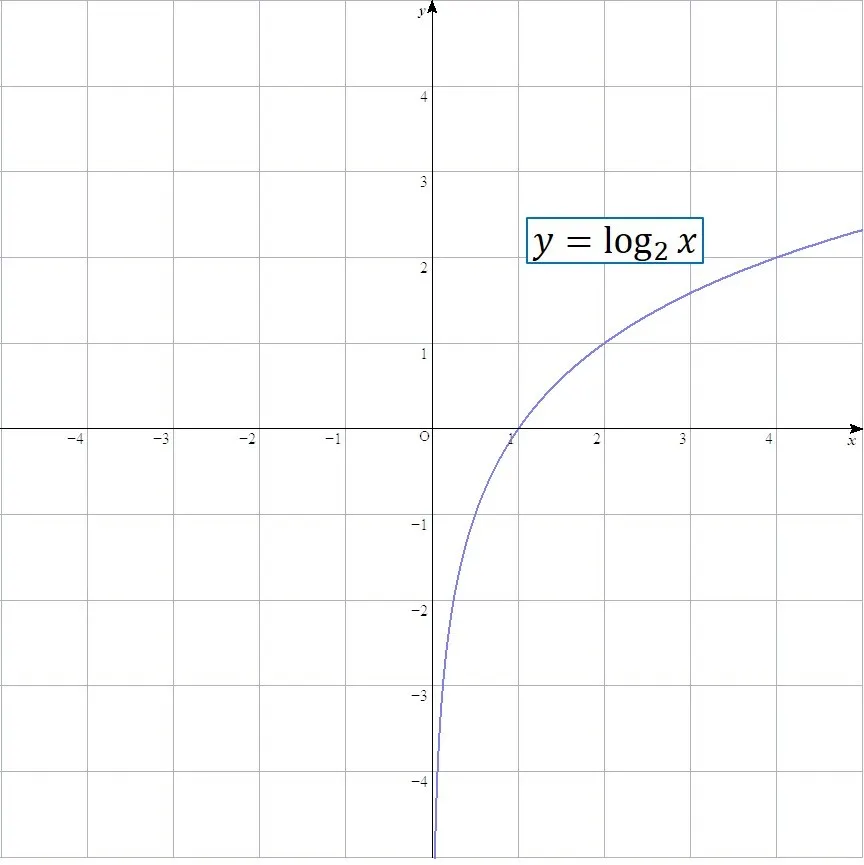
まずは，log関数の基本形のグラフに関するポイントです．
- x=1を通る
指数関数ではｙ＝１を通るというものでした．ｘとｙの関係が逆になっているので，指数関数をしっかり理解していれば，対数関数に関してもすっきりと頭に入ってくるかと思います．
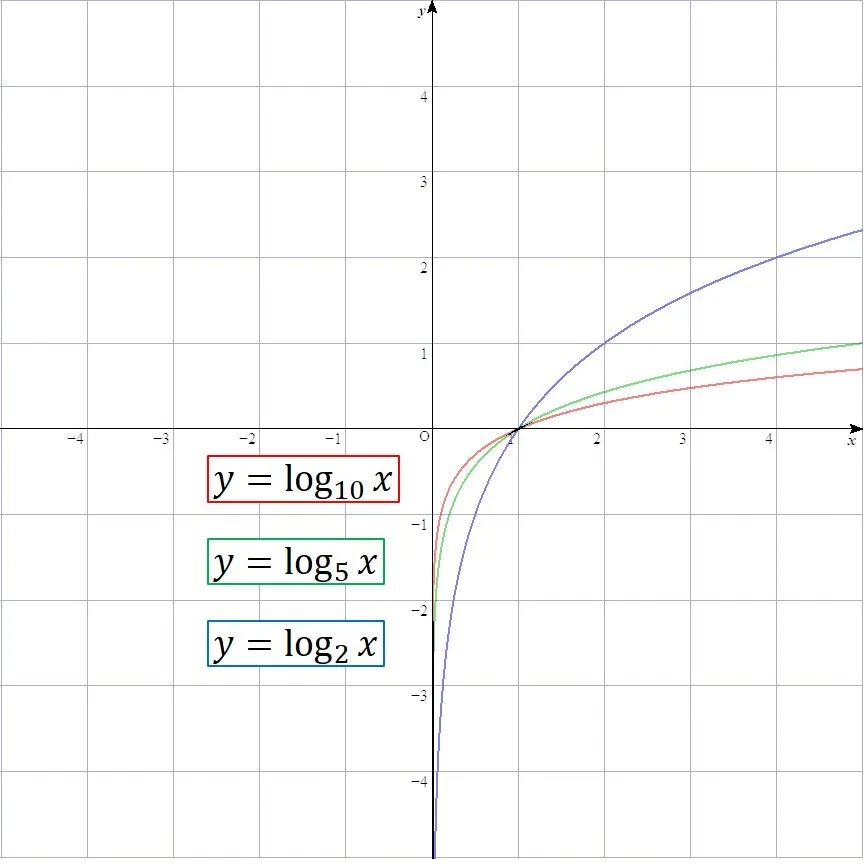
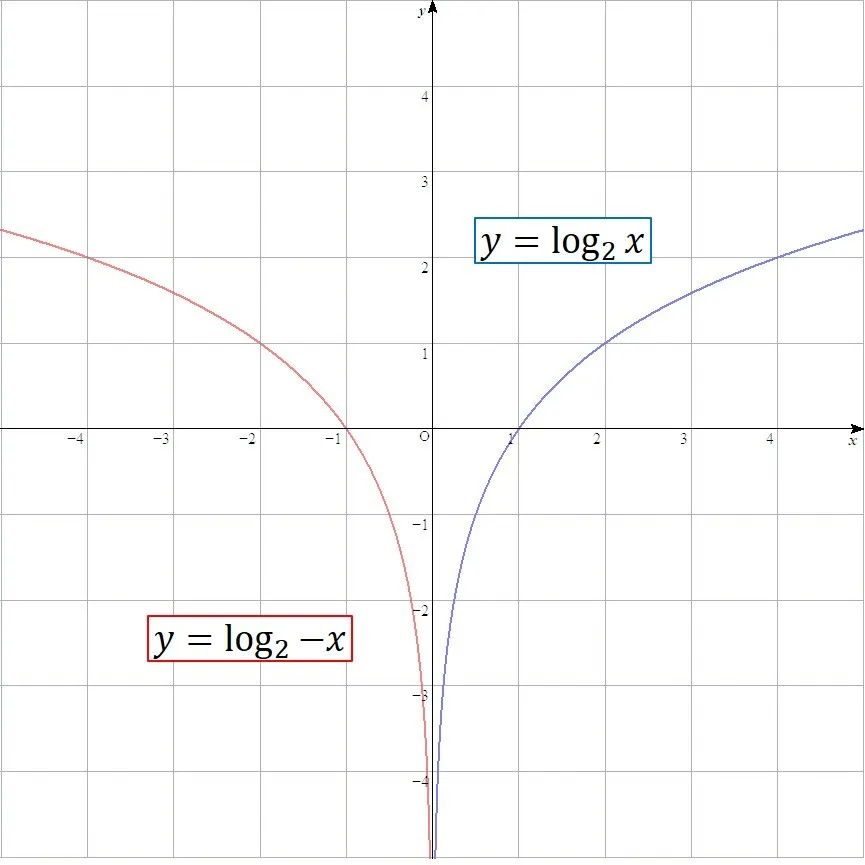
ここでは例として，a=２の場合のグラフを示します．
底：aに関して
これまでの関数と同様に，ａを変化させるとグラフの形が変わっていきます．
ただし，前回の記事と同様に注意点があります．
底：ａ＞０底は必ず正でなければなりません．
次に底を分数にしてみます．
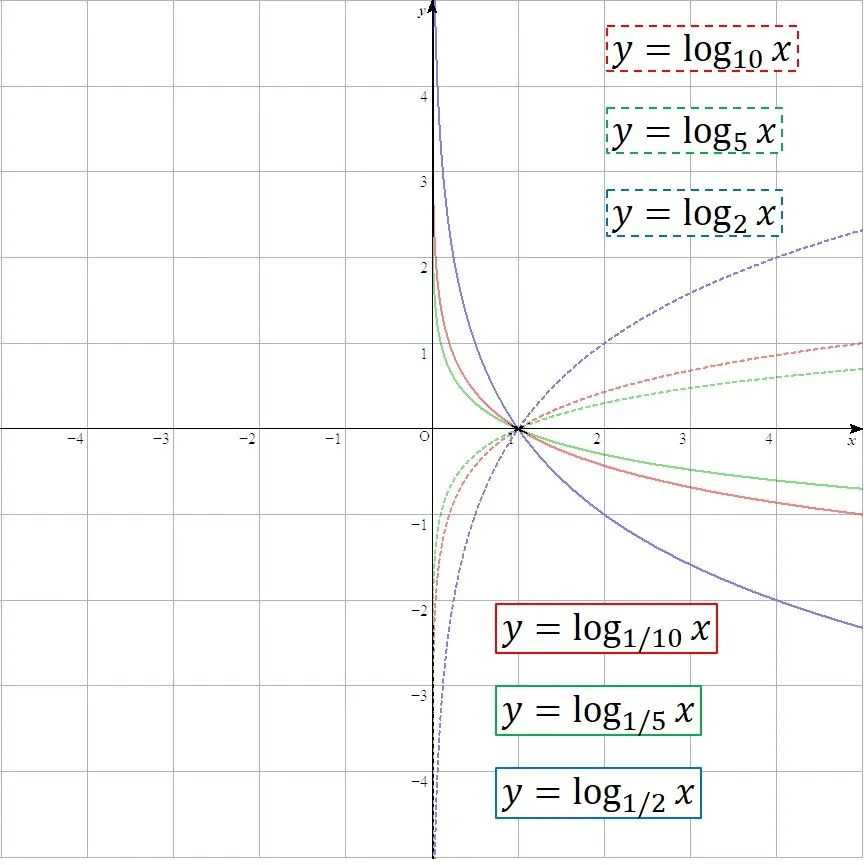
前回の記事を読んだ方は予想がつくかと思いますが，見ての通り，底を分数にすると，ｘ軸に関して対称移動したグラフになります．
例えば赤のグラフでは１/２のｙ乗がｘとなりますが，書き方を変えて，２の-y乗がｘという式にもなります．したがって，ｙの符号が負になっているので，x軸対称になりますね．
このように，字面で説明してもわかりづらいものは，グラフにしてあげるとわかり易いです．
対数のグラフは底を逆数にすると，x軸対称になる．
指数関数との関係
指数と対数を比較してみると以下のようになりますね．
このことを伝えたうえで以下の要点を押さえていきます．
対数関数は指数関数の逆関数である
このことを伝えてしまいましょう．
そして，グラフを書いて見せてみます．
指数関数と比較して並べてみましょう．
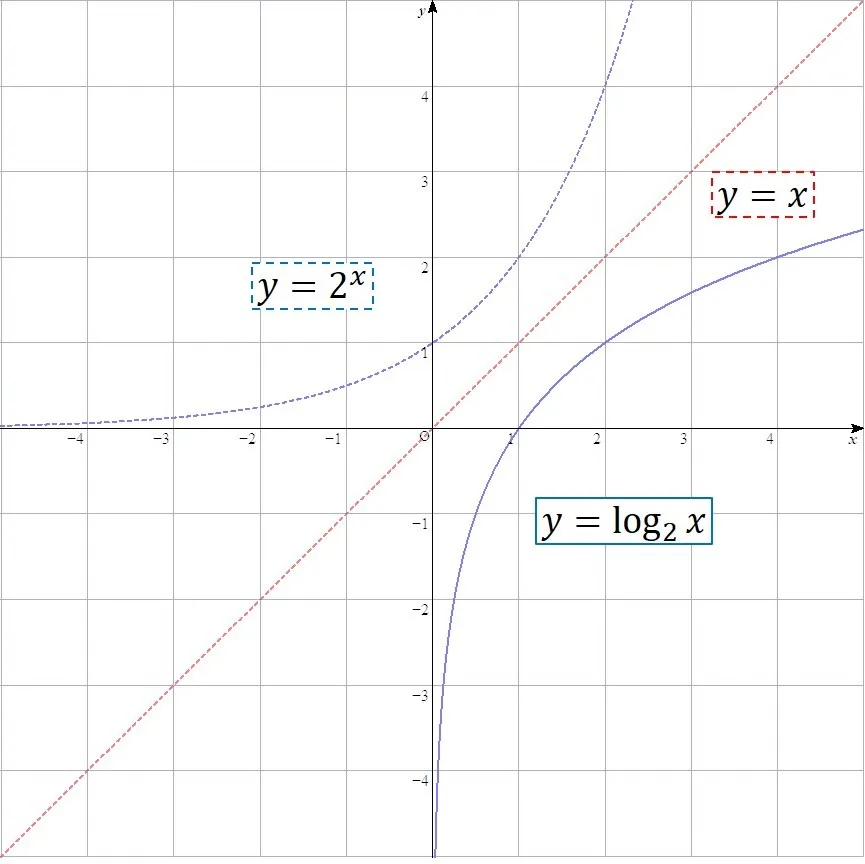
このように，見せてあげると関係がわかり易いですね．
ｘとｙの関係が逆（原点に対称，ｙ＝ｘに対称）となっていますね．
このことは底を変化させていっても同様です．
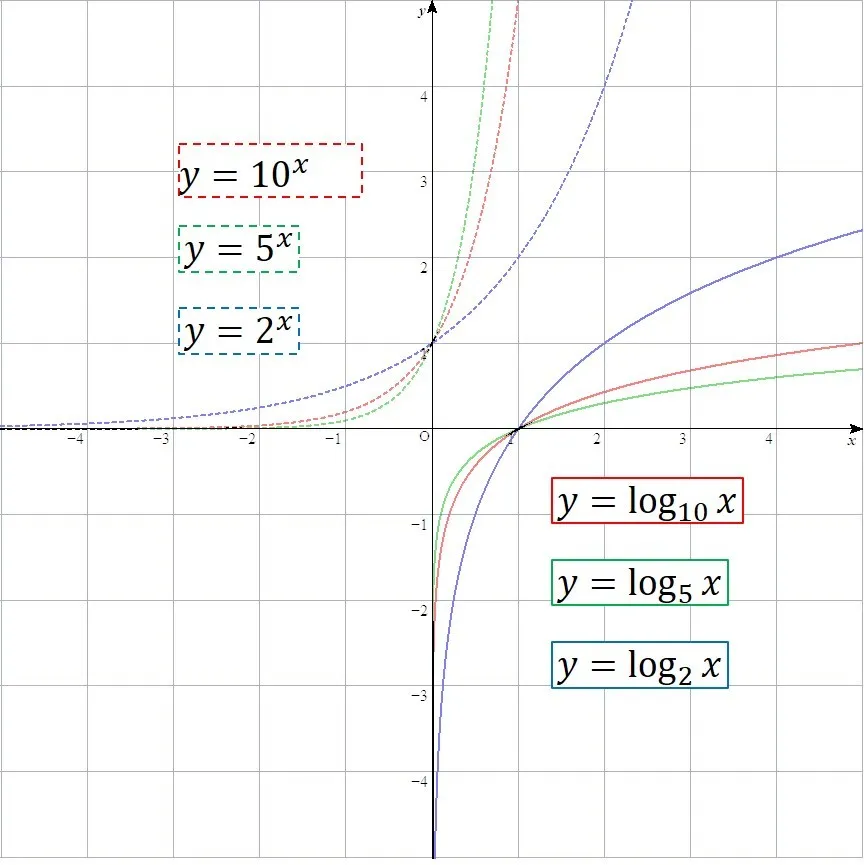
指数関数はｘの値が小さくなるほど，ｘ軸に近づいていきます．
対数関数はｙの値が小さくなるほど，ｙ軸に近づいていきます．
このように，指数関数の性質がわかっていればある程度,log関数の性質も予想がつくようになりますね．
このことを生徒には伝えていくと興味を持ってくれるのではないでしょうか．
グラフの移動
これまでの関数のグラフと同様にグラフの移動の基本は以下の図に示す通りです．
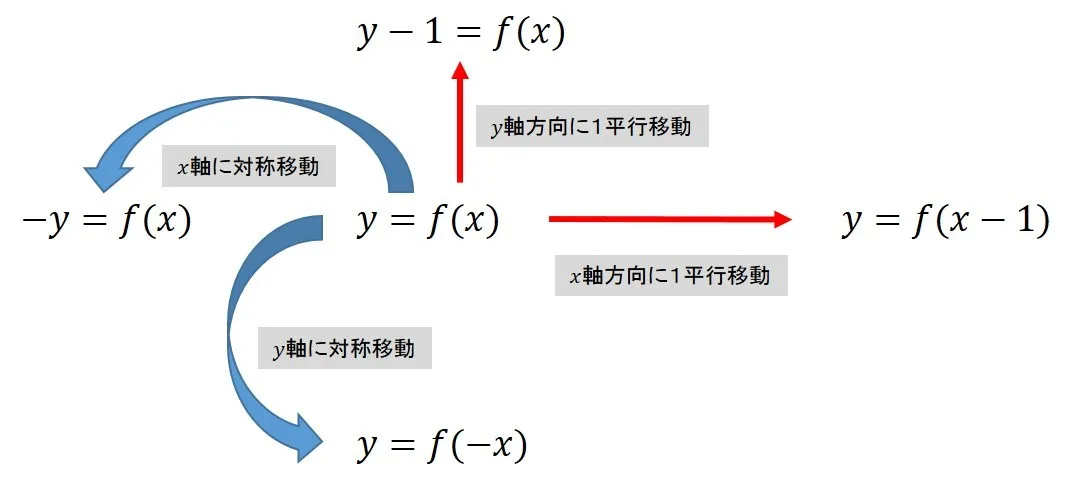
このように平行移動や対称移動をしていきましょう．
平行移動
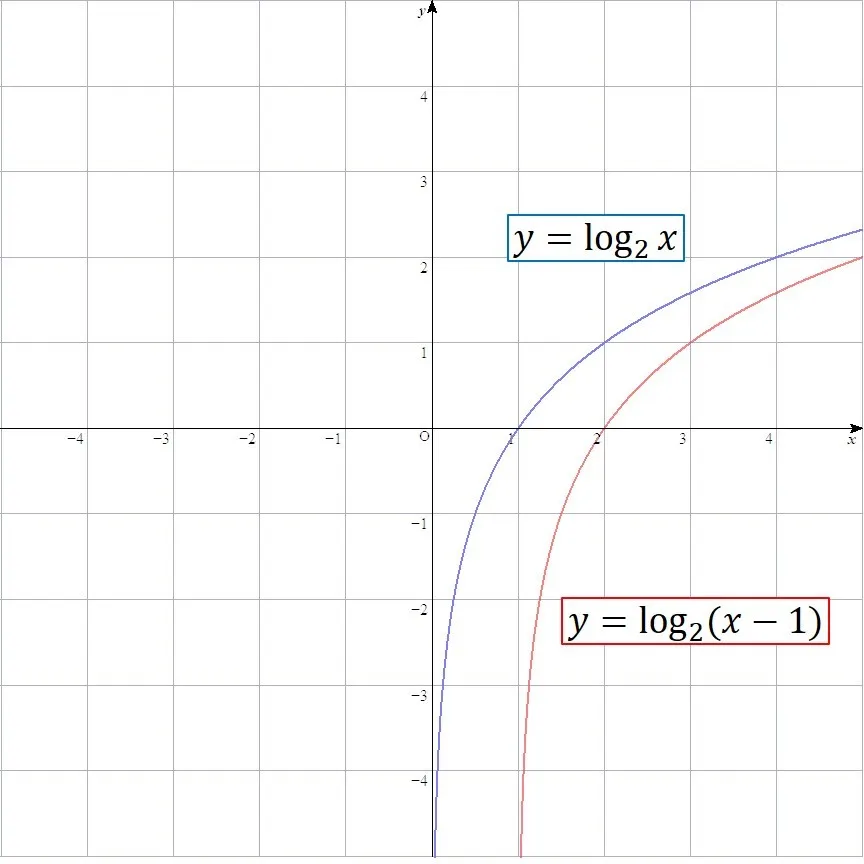
x方向
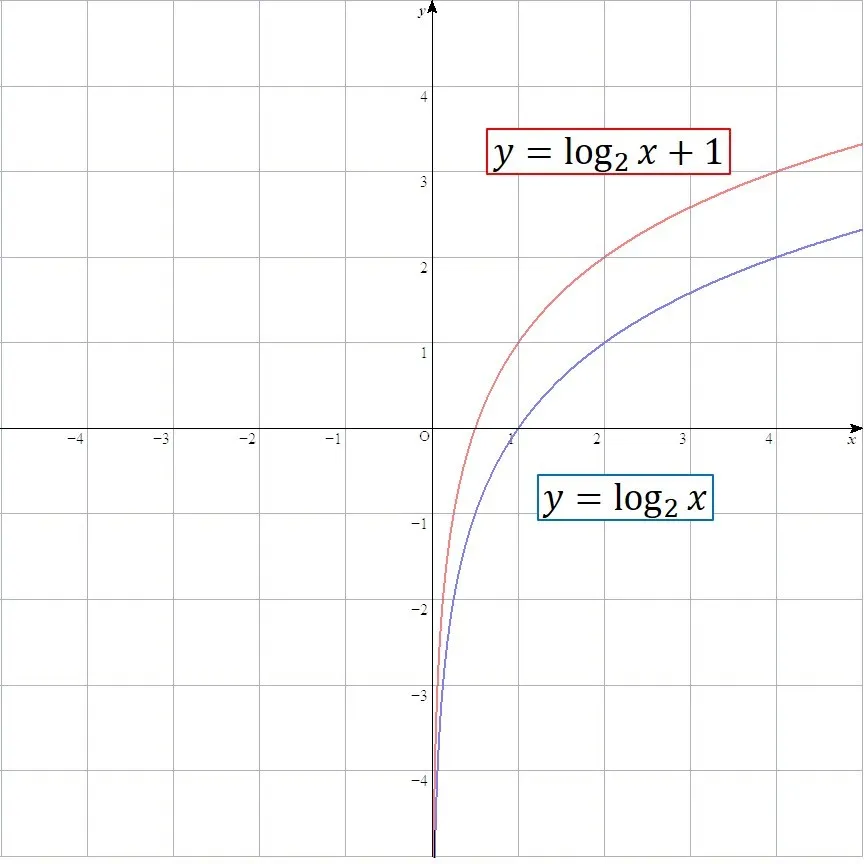
y方向
対称移動
x方向
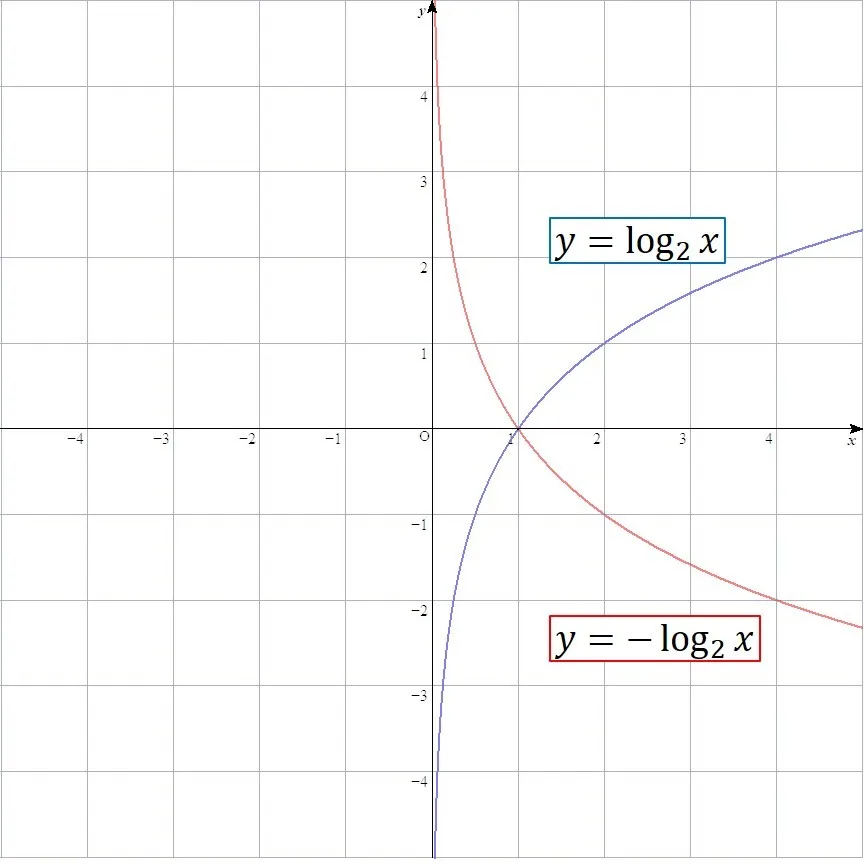
y方向
まとめ
以下に対数関数に関するまとめを記述します．
の意味：ａのｙ乗はｘ
底：ａ＞０
対数関数は桁数がわかる
対数関数は指数関数の逆関数である
対数関数は指数関数の性質をしっかりと理解しておけば，ｘとｙの関係をしっかりと理解していれば，グラフに関しては難しくはありません．
指数関数の段階でしっかりとこのことを生徒に伝えておきましょう．
そのうえで対数関数の授業を指数関数との比較で展開すると面白いと思ってくれる生徒もいることと思います．
塾講師ステーション情報局ってなに？
塾講師ステーション情報局とは、
“塾講師のお仕事をもっとわかりやすく！”をテーマに、日々記事を配信している情報サイトです。
塾講師希望者の“塾アルバイト応募への悩み解決"はもちろんのこと、
実際に塾講師に採用された後の“現場で使える指導ノウハウ"、”認識を変える驚きの記事"などをご提供しています！
そして、親サイトの「塾講師ステーション」では塾講師希望者の方々が、自分にあった職場情報や塾・教室と出会えるよう日本最大規模の求人を掲載しています。
登録すると、塾からのスカウトが届いたり、メルマガ購読による定期的な情報収集などが可能です。
もちろん、すべて無料のサービスです。
よろしければ、お気軽にご登録ください。
▼求人掲載件数9500件以上！「塾講師ステーション」へご登録はこちら
【あわせて読みたい記事】
・【数学講師向け】n+1番目…2mは偶数…"文字を使って数量を表す"分野をわかりやすく指導する方法！
