公開日 2014/08/25
更新日 2026/01/20
【数学講師向け】組立除法を使わずに因数分解を素早く行う方法【受験・お役立ち】
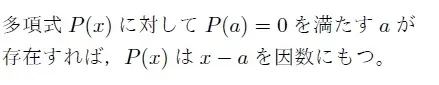
はじめに【簡単に因数分解ができる方法】
因数分解といえば組立除法による方法が一般的です。もちろんそれが最も効果的だと思います。ですが、受験においてはやはり素早く数式を解かなければなりませんね。計算をするスペースも限られています。ここでは簡単に因数分解が出来る方法を紹介します。
因数定理
因数定理とは，
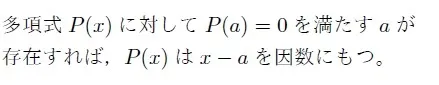
というものです。この定理により，ある多項式に数字を代入して因数を見つけることができます。
組立除法
組立除法について知らない方もおられると思うので簡単に説明します。組立除法とは割る数が１次式の整式の割り算をするときに商と余りを手際よく求める手法です。割る数が２次式以上には適用できませんが１次式の場合には効力を発揮します。その方法を紹介します。
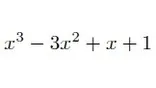を例に説明しましょう。ｘ－１で割ることを考えます。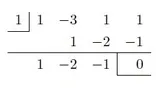
まず上の画像の右上には（割る式）＝０の解を書きます。ここでは１です。そこから１番目、…、５番目と数えることにします。
- 左４つは各項の係数を左から順に書きます。
- 左から２番目の数字を一番下にそのまま書きます。
- 左上の数字とその数字をかけて真ん中の３番目に書きます。
- 上の左から３番目の数字その下の数字を足して一番下に書きます（－２のこと）。
- 今度もそれに左上の数字をかけて真ん中の４番目に書きます。
- これを繰り返して、最後の下のかっこのところまでやります。
そのとき、下のかっこの部分に余り、その左には商がでます。
因数定理を用いた因数分解
以上で紹介した方法で組立除法よりもはやく因数分解できるかどうかは個人差があると思いますが，もしこの方法が簡単だなと思われたら使っていただければ，と思います。
