整数問題もこれで攻略！生徒に"鳩の巣原理"を教えよう！【知っていると必ず得】
絶対に得をします！
教科書にははっきりと載っていないものの、知っていて絶対に得をする数学のツール（証明法や定理）について紹介していきます。
今回は、鳩の巣原理を紹介します。
とても単純な論理ですが、証明の決め手になることがよくあります。
数学界、特に整数論の分野では数多くの定理の証明の決め手となっているようです。
鳩の巣原理とは？
m>nとする。m個のものをｎ個の箱にどのように分配しても、必ず２個以上のものが入っている箱が少なくとも１つは存在する。
これが鳩の巣原理です。
部屋割り論法や抽出し論法とも呼ばれます。
この原理を具体的に鳩の巣で例えると、巣が５つ、鳩が６羽いるときに、どう鳩を割り振っても必ず２羽鳩が入る巣が存在します。
巣の数に対して鳩がそれよりも多くいるのですからそれは当然ですよね。
こんなの改めて説明されなくたって当たり前のことじゃん！とお思いの方がいると思いますが、
この単純な論理が実に鮮やかに問題を解決してくれることがあります。
実際に鳩の巣原理を用いて解ける入試問題を見てみましょう。
鳩の巣原理で鮮やかに問題を解く！
（１）次の文章は、ある条件を満たすものが存在することを証明する際によく使われる「鳩の巣原理」（または抽出し論法とも言う）を説明したものである。（説明略）この原理を用いて、以下の①②を証明せよ。ただし、証明はこの原理をどのように用いたかをわかるようにせよ。①１辺の長さが２の正三角形の内部に任意に５個の点をとったとき、そのうちの２点で距離が１よりも小さいものが少なくとも１組存在する。②座標空間内で、その座標が全て整数である点のことを格子点という。9個の格子点が与えられたとき、そのうちの2点の中点がまた格子点となっているものが少なくとも1組は存在する。（広島大）
（２）任意に与えられた相異なる４つの整数m1,m2,m3,m4から、適当に2つの整数を選んでその差が3の倍数となるようにできる。このことを証明せよ。（神戸大）
鳩の巣原理を知っていれば、これらの問題はすぐ解けます。ぜひ少し立ち止まって考えてみてください。
・・・
・・・
・・・
・・・
それでは解答です。
（１）①1辺の長さが2の正三角形は、図のように1辺の長さが1の正三角形4つに分割することができる。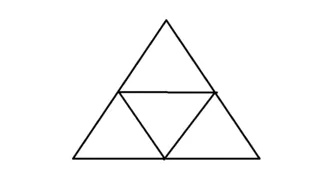
正三角形の内部に任意に5個の点をとったとき、鳩の巣原理より5点のうち少なくとも2点が同じ小正三角形の内部か線上に存在する。この2点の距離は明らかに1よりも小さい。
よって題意は示された。
②座標空間上の格子点の偶数、奇数のパターンについて、
（x,y,z）=(偶、偶、偶)（偶、偶、奇）（偶、奇、偶）（偶、奇、奇）（奇、偶、偶）（奇、偶、奇）（奇、奇、偶）（奇、奇、奇）の8通りが考えられる（偶数は偶、奇数は奇と表した）。
偶数と偶数、奇数と奇数の和が偶数となるから、格子点と格子点の中点がまた格子点となるには、2点のｘ座標、ｙ座標、ｚ座標の偶奇が完全に一致すればよい。
鳩の巣原理より、9個の格子点が与えられたとき少なくとも2点が同じ偶奇のパターンになる。
この2点の中点は格子点となる。
よって題意は示された。
（２）整数を3で割った余りで分類すると、ｋを整数として｛3k｝｛3k+1｝｛3k+2｝の3種類のグループに分類できる。相異なる整数が4つ与えられたとき、鳩の巣原理より同じグループに属するものが少なくとも2つ存在する。
それらをm_i=3a+r,m_j=3b+rとおく（i,jは１～４のいずれかの整数。a,bは整数で、rは０～２のいずれかの整数）。
m_iとm_jの差をとると、3a+r-（3b+r）=3(a-b)となり、a-bは整数だから３（a-b）は3の倍数。
よって題意は示された。
頭の働かせ方のポイント
これはわざわざ鳩ノ巣原理と命名しなくても当たり前のことを言っているわけですが、
実はその感覚が大事です。
自分で状況を漏れなくだぶりなく網羅できる場や規則をつくり問題を言い換えるだけで、数学を解く際のアプローチのしかたも変わり、より取り組みやすくなるのではないでしょうか？
ぜひ「鳩ノ巣原理」を生徒さんの頭の引き出しに入れてあげてください！
【あわせて読みたい記事】
・【数学講師向け】不等式の基本をおさえるー不等式の意味・解き方
・【数学講師必見】関数のグラフに関する指導の要点まとめ！～2次関数～
