【正弦定理と余弦定理】定理を忘れても大丈夫!自力で導けるようになろう!
今回は高校数学の初期で学ぶ三角関数の分野における重要定理、正弦定理・余弦定理を紹介します。有名な定理ですが、肝心の式は少し記憶が曖昧になることもしばしば。
そんな生徒さんがもしテストなどの場で公式を忘れてもすぐ思い出せるように、「なぜあんな式になるのか?」を定理の証明から紹介していきたいと思います。数ある方法の中からなるべく簡単なものを選びましたので、ぜひ生徒さんにこの証明方法を教えてあげてください!
正弦定理の導出方法
まずは正弦定理を提示します。
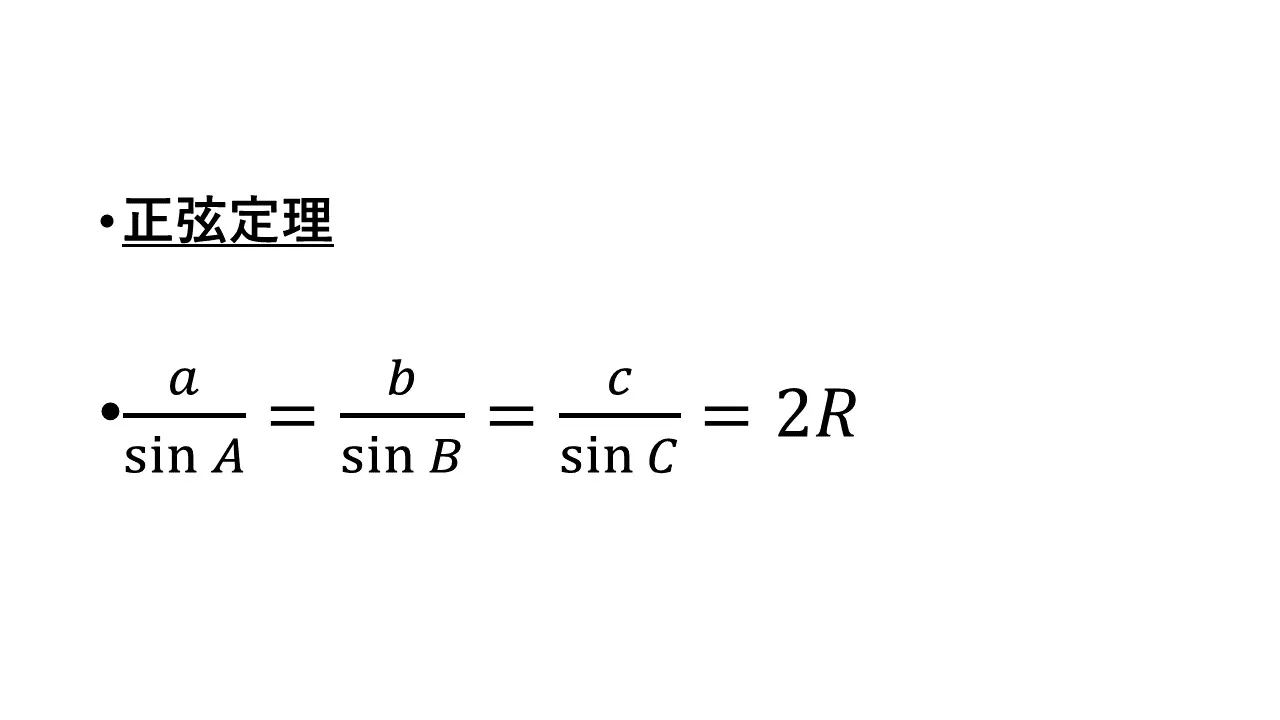
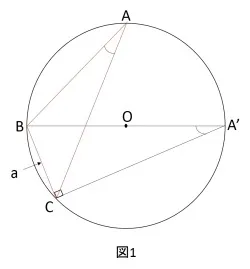
こちらは余弦定理に比べて図で直感的に理解できる分容易です。正確には3パターンに分けることができますが、基本は全て変わらなくて「三角形に対して外接円を描くこと」です!

∠Aが鋭角の場合
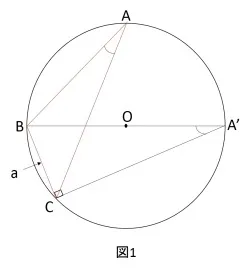
この場合は上図(図1)のようになります。元々の三角形ABCがあり、さらに線分BOの延長線と外接円の交点をA'とします。すると円周角の定理より
∠BAC = ∠BA'C となります。もちろん sinA = sinA' となります。図にも書きこんでありますが、BA'が外接円の直径なので∠BCA'は直角になっています。よって
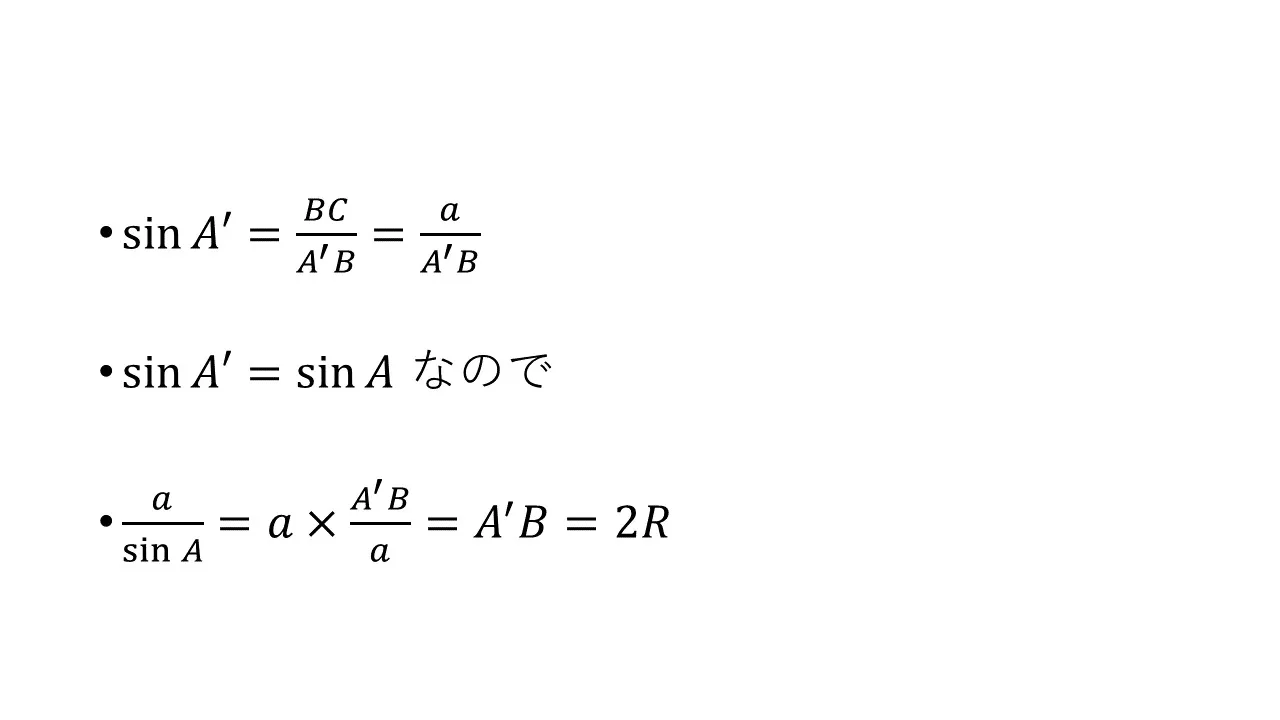
∠Aが直角の場合
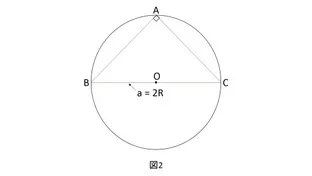

以上で∠Aが直角の場合も正弦定理を導き出すことができました。
次に∠Aが鈍角の場合も説明していきます。
∠Aが鈍角の場合
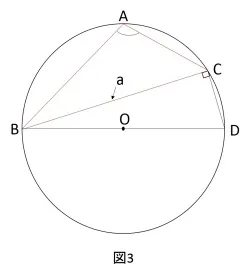
この場合に関しては線分BOを延長して、外接円との交点をDと置きます。すると四角形ABCDは円に内接する四角形となるので、∠A + ∠D = 180°となります。 次に余弦定理の導出方法を確認しておきます。
次に余弦定理の導出方法を確認しておきます。
余弦定理の証明方法
そもそも余弦定理とはどんな公式だったでしょうか?一度振り返ってみます。

次に、この定理をどのように用いるのか、問題を解いてみましょう。
⊿ABCの∠Aが鋭角の場合
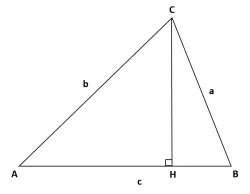
計算ベースで機械的に思い出すことができる証明方法を紹介します。右のような三角形をイメージします。以下では
a² = b² + c² -2bc cosA を証明していきます。

⊿ABCの∠Aが直角の場合

⊿ABCの∠Aが鈍角の場合
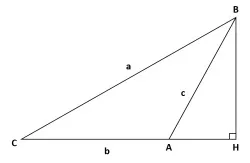
この場合は上図のようになります。ここも∠Aが鋭角の場合と同じで、最終的には三平方の定理を用いることに帰着します。

となります。以上で全ての場合において余弦定理が証明されました!
学校ではあまり証明まで教えてくれないことが多いですが、やはりいざ「公式を忘れた!」という場合に生徒が自力で思い出せるように証明を知っておくことは重要です。ぜひ生徒さんに教えてあげてください!


![10円玉をピカピカにしよう!![高校化学]](https://www.juku.st/cdn/article_images/304/large_juku_entry_images_image.webp)