【数学講師向け】不等式の基本をおさえるー不等式の意味・解き方

不等式の意味とは？

不等式には大きく分けて3つの意味があります。

・単なる大小関係を表す時に使う

・解集合を表す

・取りうる値の範囲を表す

・大小関係

例えば、a≧bは　a>bまたはa=b　の少なくとも一方が成り立つと主張しているだけです。

したがって、3>1と3≧1のうち、正しいのはどれか？　という問題を出したときの答えは「どちらも正しい」となります。

・解集合 

x^2-3x+2=0 を解くとxは1と2となり、{1,2}という解集合が求められます。

「=」を変えて「<」とすると、

x^2-3x+2<0 となり、xの解は1<x<2となり、1<x<2を満たすx全体が解となります。

詳しくは後ほど例題①を参照してください。

・取り得る値の範囲

実数xが1と2の間のすべての値をとって動くことを1<x<2と表す場合があります。

例えば、-1<x<1 , -1<y<1としたとき、x-yの取りうる値の範囲を不等式で表してみましょう。

 

辺ごとに引き算すると0<x-y<0 となり、

取りうる値の範囲としては間違いになってしまいますね。

 

また、数Ⅱの範囲の例だと、

x^2+y^2=1 のとき、-1≦x≦1,-1≦y≦1は単なる大小関係としても、取りうる値の範囲としても正しいですが、これらを辺ごとに加えた-2≦x+y≦2は取りうる値の範囲としては間違いとなります。

 

 

※実際の値域は-√2≦x+y≦√2となります。実際、x+y=k とし、y=-x+k をx^2+y^2=1 に代入して整理すると、接点の値(±1/√2, ±1/√2)　が得られ、x+y=k に代入することで求められます。

下図では直線y=-x+kが円と接する状態を示しています。このときのy切片がkの値の取りうる範囲の最大最小となります。y軸上に-√2≦k√2となるところを太線で示しています。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

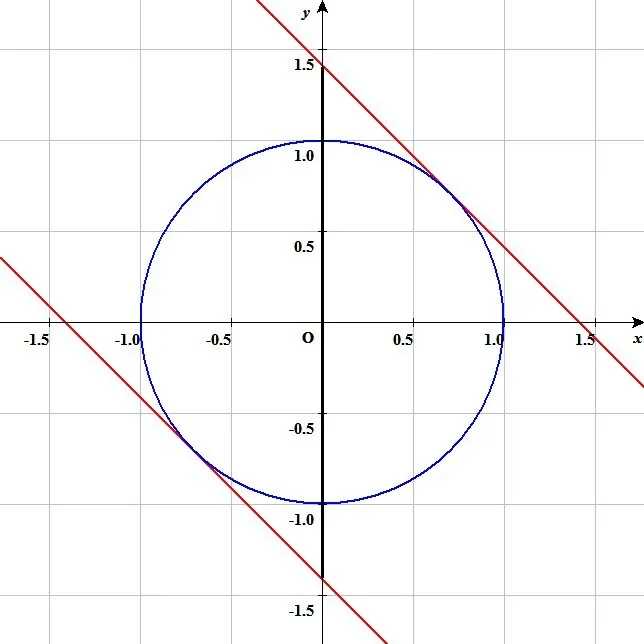
「すべての値をとって動く」という問題は入試問題で取り上げられやすく差がつく問題です。

  

「値をとって動かすことができること」⇔不等式で表現できること

を意識して教えるようにしましょう。

 

 

不等式を解くときにはこのような特徴があり、先生から教えられるばかりではなかなか力がつきにくく、「生徒に考えさせる」ことが肝要になってきます。

例えば、日本工大の入試問題を取り上げてみましょう。

 

例題①　　　

次の不等式を解け。

 

この不等式は「解集合」を表しています。

 

したがって、左辺が右辺より小さい範囲が解集合です。

絶対値がついているということで、場合分け　というのはあくまで基本の考え方です。

試しに場合分けを使って解いてみると

 

ⅰ) x>0 のとき、　

 

 

 となり、下図の色のついた部分になります。

図から0より小さい部分は0<x<4 となります。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ⅱ)x≦0 のとき、　

 

となり、下図の色のついた部分になります。図から0より小さい部分は

-4<x≦0 となります。

以上を合わせると、-4<x<4 が答えである。

となり、かなり手間がかかってしまいます。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

他のやり方としては主に2通りあり、

 

Ⅰグラフを用いる　

Ⅱうまく式変形を行う

 

があります。

Ⅰではグラフのかき方はいくつかあります。

 

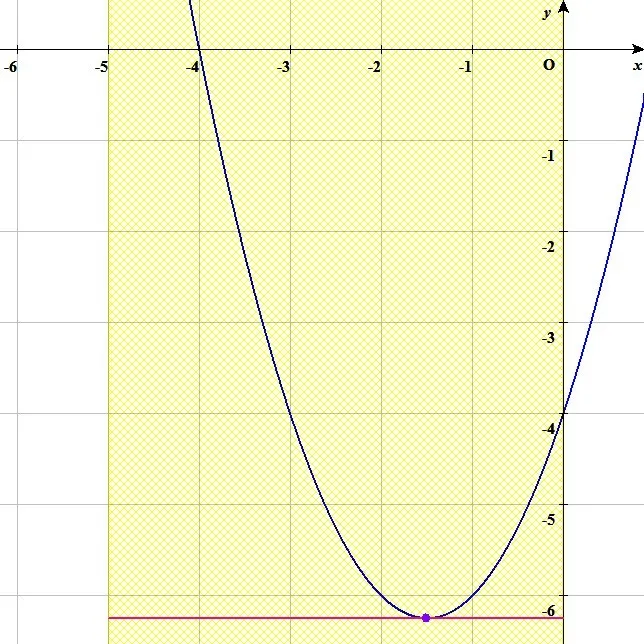
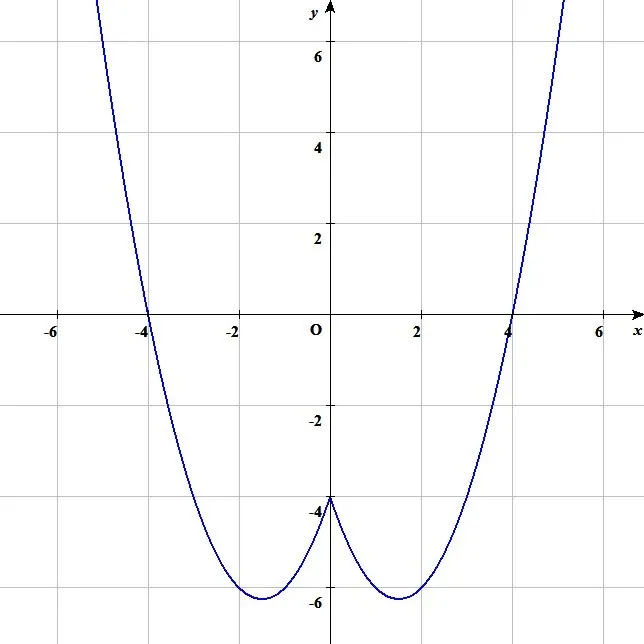
左辺をそのまま　

とすると下図のようになるので図から答えを導くこともできます。

ただ、このグラフを一発ではなかなか生徒はかけないでしょう。

 

 

 

 

 

 

 

 

 

 

 

 

一方で、不等式を変形し、

 

とし、

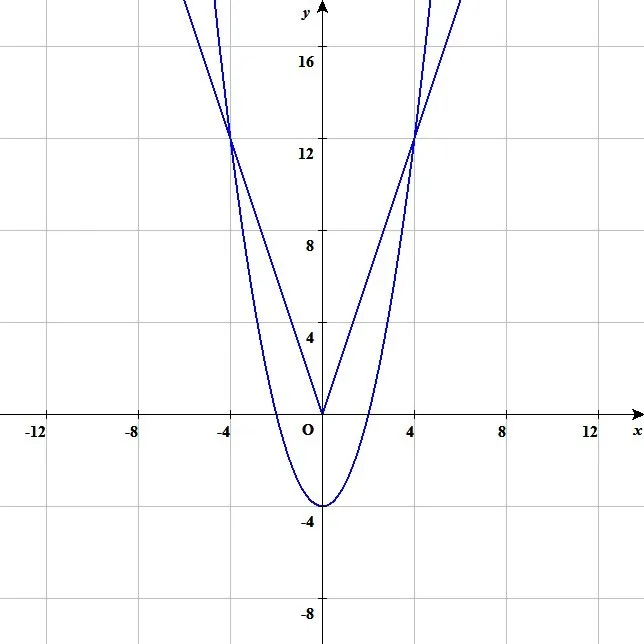
として絶対値のグラフと普通のグラフの2通り書くのは下図のようになり、かきやすさ・分かりやすさが失われていません。

式変形がどのような意味を表しているのか考えずに闇雲に問題を解く生徒が多いので、私たちが俯瞰して問題を眺める視点を持つように図示することも必要です。

 

 

 

 

 

 

 

 

 

 

 

ここまでⅠのグラフを使って解くを説明してきました。グラフも４つも書いて長々とした説明になりました。

 

 

さて、実はⅡの式変形ではこれまでの苦労を考えると驚くほど簡単に求められます。ポイントは　

 

と考えることです。

その結果、(|x|-4)(|x|+1)<0と因数分解でき、

|x|+1 は常に正なので結局|x|-4<0 を解くだけです。

以上より-4<x<4と簡単に求められます。

 

このように不等式を示すときにもう1つ重要なことは「不等式を変形するセンスを磨く」ということです。

もう1問見てみましょう。

例題② 

a≦0,b≦0のとき、を示せ

 

この不等式の表す意味は「単なる大小関係」を表しています。素直にやれば

 

(右辺)-(左辺)=-1

と変形できるのでb<0 より2のb乗は1より小さいので正である。

累乗は全て正なので右辺-左辺+1は正であるとなり、手詰まりになってしまいます。

この問題は式変形に慣れている人だと

 

 

と右辺を左辺に集めて因数分解の形に変形できます。

 

答案を見てしまえば「なんだ、それだけか」と生徒も思うはずです。

ですが、実際に自分で思いつくとなるとなかなか慣れないと解けない問題です。

「～を示せ」問題のときは目標が何か分かっているのですからゴールにたどりつくために何が必要なのか、を論理的に導く練習を行わせるようにしましょう。